[科普中国]-类方程

类方程是数学术语，设 G 为有限群，群 G 的元素按共轭关系分成一个个共轭类。类方程是指有限群的阶与其共扼类的长度之间的一个等式。

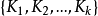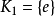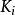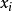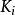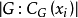简介设 G 为有限群，群 G 的元素按共轭关系分成一个个共轭类。设是 G 的全部共轭类。习惯上。在每个共轭类中取一个代表元，于是共轭类的长度为。进而有

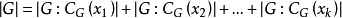
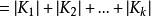
上面的等式称为 G 的类方程。1

共轭互为共轭的子集在同一轨道里，这个轨道一般叫做共轭类，共轭类中的元素互为共轭。子集S的稳定子满足gSg−1=S，它也称为S的正规化子，记作N(S)，它是一个子群。这样一来，共轭类的中的元素和N(S)的陪集一一对应，每个共轭类中有[G:N(S)]个元素。进一步地，共轭类中每个元素的正规化子有N(gSg−1)=gN(S)g−1，它们也形成一个共轭类。

首先，以上X中可以只取那些只有一个元素的子集，这个情况等价于X=G，这就相当于定义了群元素间的共轭关系。群的元素在共轭的作用下分成了多个等价类，而不动元素FG显然就是中心C。如果中心元有c个，其它等价类Ck分别有ck个元素（k=1,2,⋯,m），则类方程变成：G=C∪C1∪C2∪⋯∪Cm，|G|=c+c1+c2+⋯+cm。

其次，还可以把X中的元素限定为子群，这就定义了共轭子群。共轭子群具有共轭子集一样的性质，只是在子集和其正规化子的关系上有本质不同。对一般子集，不一定有S⊆N(S)，而对于子群H不仅有H⊆N(H)，还有H⊴N(H)。从另一个角度看，N(H)其实是通过缩小G来使H成为正规子群，N(H)是G中使H称为正规子群的最大子群。考察H的所有共轭子群之交K=∩Hk，可以证明aHka−1任然包含所有H的共轭子群，从而恒有aKa−1=K，即K为正规子群。特别的，如果H的指数有限，则K的指数也有限。

相对于单个元素的正规化子，子集的正规化子其实是被弱化的。正规化子N(x)是所有满足axa−1=x的元素，即所有与x可交换的元素。为此可以定义与子集S所有元素可交换的集合，称它为S的中心化子，并记做C(S)。容易证明它也是子群，并且有C(S)⊴N(S)成立。而对单个元素显然有：C(x)=N(x)。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学