[科普中国]-组合最优化问题

概述

组合最优化问题（combinatorial optimizationproblem）是一类在离散状态下求极值的问题。把某种离散对象按某个确定的约束条件进行安排，当已知合乎这种约束条件的特定安排存在时，寻求这种特定安排在某个优化准则下的极大解或极小解的间题。组合最优化的理论基础含线性规划、非线性规划、整数规划、动态规划、拟阵论和网络分析等。组合最优化技术提供了一个快速寻求极大解或极小解的方法。

基本原理组合最优化是通过对数学方法的研究去寻找离散事件的最优编排、分组、次序或筛选等，是运筹学中的一个经典且重要的分支，所研究的问题涉及信息技术、经济管理、工业工程、交通运输、通信网络等诸多领域。该问题可用数学模型描述为：

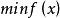
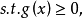
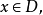其中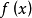，为目标函数，为约束函数，为决策变量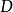，表示有限个点组成的集合。

一个组合最优化问题可用三参数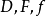（）表示，其中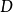表示决策变量的定义域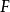，表示可行解区域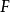，中的任何一个元素称为该问题的可行解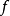，表示目标函数。满足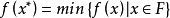的可行解称为该问题的最优解。组合最优化的特点是可行解集合为有限点集。由直观可知，只要将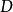中有限个点逐一判别是都满足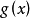的约束和比较目标值的大小，该问题的最优解一定存在和可以得到。因为现实生活中的大量最优化问题是从有限个状态中选取最好的，所以大量的实际优化问题是组合最优化问题。1