[科普中国]-诱导同态

诱导同态是线性映射在张量代数上的开拓。诱导同态满足的自然性，是同伦群的一个重要性质。

定义介绍任意一个带基点的空间之间的映射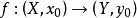在同伦群上有诱导同态 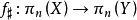，它满足以下性质：如果还有映射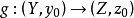，则。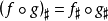

诱导同态满足的这个性质称为是自然性，这是同伦群的一个重要性质。

同伦群[homotopy group]

设 X 是一个带基点拓扑空间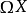， 是 X 上保基点点闭道路空间，其基点是取值于基点的常值道路。归纳定义。

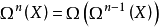定义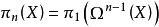

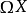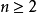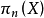由于是 H 空间，而 H 空间的基本群是交换群，因而当 时， 交换群。

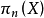中的元素可用 n 维球面到 X 的映射作代表。这个映射作用在这个 n 维球面道基本类上给出 X 的 n 维同调到一个元素。从而给出群同态，称为胡雷维奇同态：

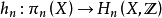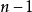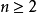关于同伦群的第一个一般结构是所谓的胡雷维奇定理：如果 X 是 连通的且，则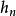 是同构。另一个重要的一般结果是弗罗伊登塔尓（Freudenthal）维悬定理：当 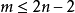时,有。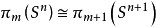

CW 复形的同伦群具有很好的性质：CW 复形间的连续映射 是同伦等价当且仅当它是弱同伦等价。从一个拓扑空间 X 到拓扑空间 Y 的一个映射称为弱同伦等价(weak homotopy equivalence) 如果对任意的 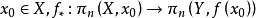是同构。

基本群的定义是庞加莱在1895 年提出的。此后很多人想到过高维的推广，这些人中包括: 亚历山大、切赫、德恩等。但都因为初步性质过于简单以为不能导致深刻结果而被放弃。第一个正式的定义是胡雷维奇在1935 年莫斯科国际拓扑会议上提出的。除可缩空间外，最简单的空间就是球面 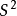。胡雷维奇定理给出了第二个同伦群，其实在同伦群的定义被提出之前，霍普夫早在1930 年就本质上算出了 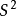的第三个同伦群。很明显同调论不足以区分这个群中的同伦类。但是同伦群并未因此马上被提出，这是值得深思的事情。20 世纪50年代初，嘉当、塞尔等利用纤维化的[上] 同调谱序列，提出了研究同伦群的新方法并取得了球面同伦群计算的突破性进展。此后包括同伦群研究的同伦论成为数学的中心研究领域之一并在许多领域获得重要应用。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学