[科普中国]-普吕克坐标

概念

普吕克坐标是格拉斯曼空间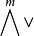 中可合元素的坐标。若{e1，e2，…，en}是V的基，则 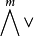的可合元素v1∧v2∧…∧vm可表示为：

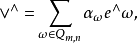
可合元素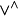 的坐标{aω|ω∈Qm，n}称为子空间〈v1，v2，…，vm〉的普吕克坐标。存在着许多判别 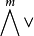的元素为可合元素的充分必要条件，通常就是判别坐标{aω|ω∈Qm，n}为普吕克坐标的充分必要条件。例如，若

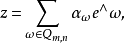为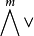 的任一元素，则z为可合元素的充分必要条件是存在m×n的矩阵A=(aij)使得：

aω=det A[1，2，…，m|ω] (ω∈Qm，n)，其中A[1，2，…，m|ω]表示A的ω(1)，ω(2)，…，ω(m)列子方阵。

格拉斯曼空间格拉斯曼空间亦称反对称张量空间。是一个最常见的张量对称类，即当G=Sm，χ=ε(符号特征标)时的张量对称类。通常写为：1

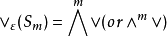
可合元素则写为：

T(Sm，ε)v∧=v∧=v1∧v2∧…∧vm，

又称为v1，v2，…，vm的外积。反对称张量空间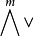 具有许多很好的性质。例如，v1∧v2∧…∧vm≠0的充分必要条件是v1，v2，…，vm线性无关；又如：

v1∧v2∧…∧vm=au1∧…∧um≠0的充分必要条件是〈v1，v2，…，vm〉=〈u1，u2，…，um〉且维数是m。也有：

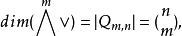其中n=dim V。若{e1，e2，…，em}是V的基，则{e∧ω|ω∈Qm，n}是 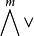的基。例如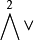 的基为{e1∧e2，…，e1∧en…，ei∧ej，…，en-1∧en}(其中i