独立代表系(system of independent representatives)是代表系的一种,Rado推广了相异代表系(SDR)的概念,建立了独立代表系的理论。
独立关系的概念设S是一个集,S的一个独立关系是一个关系序列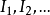 ,其中
,其中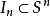 (
(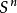 是S的n次卡氏幂集,即S的n元序列,简称n塔,即
是S的n次卡氏幂集,即S的n元序列,简称n塔,即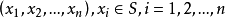 的集),因而
的集),因而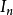 是S 上的一个n元关系,满足下面特性:
是S 上的一个n元关系,满足下面特性:
(i)若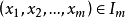 ,则必有
,则必有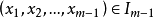 ;
;
(ii)若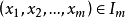 ,则必有
,则必有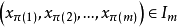 ,对{1,2,…,n}的任何置换
,对{1,2,…,n}的任何置换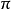 都成立。
都成立。
(iii)若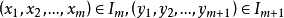 ,则必存在
,则必存在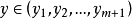 ,使
,使
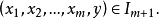
(iv)对于任何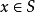 ,必有
,必有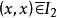 。
。
设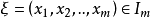 ,则
,则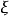 就叫做独立的。否则,就是相关的。
就叫做独立的。否则,就是相关的。
由定义可知,一个独立序列的子序列也是独立的。独立序列与序列的次序无关,而且,只要序列中含有相等元,则该序列就是相关的。
我们可以举出独立关系的例子。
把独立关系解析为不等关系,则上述(i)一(iv)条件满足,因为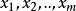 均相异,则
均相异,则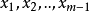 必相异,满足(i)。相异关系与元的次序无关,满足(ii)。
必相异,满足(i)。相异关系与元的次序无关,满足(ii)。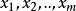 相异,且
相异,且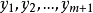 亦相异,则后者之中至少有一个y与
亦相异,则后者之中至少有一个y与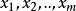 都相异,满足(iii)。因为
都相异,满足(iii)。因为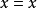 ,所以
,所以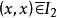 ,满足(iv)。
,满足(iv)。
又如,我们可以把S解析为一个向量空间,独立关系解析为向量的线性独立关系,即若向量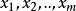 线性独立,则
线性独立,则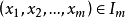 。反之,若
。反之,若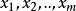 线性相关,则
线性相关,则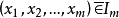 ,这亦满足(i)-(iv)条件。因为,若
,这亦满足(i)-(iv)条件。因为,若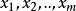 线性无关,则
线性无关,则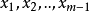 亦线性无关,满足(i)。线性无关的特征与向量的顺序无关,满足(ii)。若
亦线性无关,满足(i)。线性无关的特征与向量的顺序无关,满足(ii)。若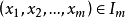 ,即
,即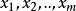 线性无关,又若
线性无关,又若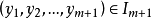 ,即
,即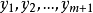 亦线性无关,如果不存在
亦线性无关,如果不存在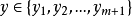 使y与
使y与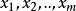 线性无关,即任一个
线性无关,即任一个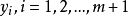 都与
都与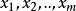 相关,则
相关,则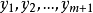 亦必线性相关,与所设矛盾,满足(iii)。最后,向量x与自身线性相关,满足(iv)。
亦必线性相关,与所设矛盾,满足(iii)。最后,向量x与自身线性相关,满足(iv)。
集S的子集序列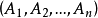 叫做具有Hall特性(Hall条件的推广),如果对于每个
叫做具有Hall特性(Hall条件的推广),如果对于每个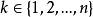 ,子集
,子集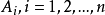 中的任何k塔的并集必包含
中的任何k塔的并集必包含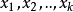 使
使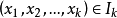 1。
1。
独立代表系的概念设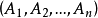 是集S的子集序列,
是集S的子集序列, 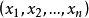 叫做
叫做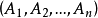 的一个独立代表系(简称为SIR),如果
的一个独立代表系(简称为SIR),如果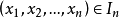 且
且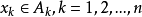 。
。
若把独立关系解析为不等关系,则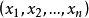 相异,且
相异,且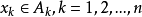 ,故
,故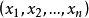 为子集族
为子集族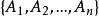 的一个SDR,由此可见SIR是相异代表系(SDR)的一个推广。
的一个SDR,由此可见SIR是相异代表系(SDR)的一个推广。
下面给出子集序列存在一个SIR的充要条件。
定理(Rado) 集s的非空子集序列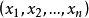 有一个独立代表系(SIR)的充要条件是
有一个独立代表系(SIR)的充要条件是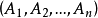 具有Hall特性1。
具有Hall特性1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国