[科普中国]-阿达马设计

定理1对于任意大的值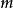，特别地对于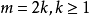，存在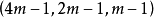的设计。（此定理的证明可见下文定理2）。

定义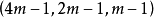设计称为维数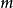的阿达马设计(Hadamard design of dimension m)。阿达马设计在错误校正码理论中非常重要2。

寻找错误校正码的一个方法是，首先集中精力寻找一个丰富的代码字集合C，然后在C中实施信息编码。

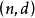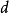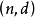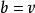一个代码有长度为n的代码字，而且两个代码字之间的最小距离是，构建代码的一个有效方法是使用设计的关联矩阵，这个关联矩阵的每一行有个1，而其余项都是0，行的长度为，任意两行在一列上同时为1的数量正好是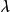个，对于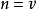。这样的行可以定义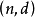代码的代码字。那么，d是多少?让我们考虑两行，比如说第i行和第j行，存在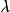个列，在这些列上，这两个行有1。在每一个行上有k个1，因此存在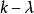个列，在这些列上行i有1而行j有0，而且存在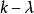个列，其中行i有0，行j有1，所有其他的列在两行上有0，所以这两行有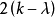个位置不同。这一结论对每一对行都成立，所以

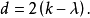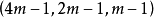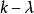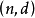对于任意大的m，存在维数m的阿达马设计，即设计。所以，对于任意大的，我们可以找到设计，因此，对于任意大的d，有代码。对于给定维数m的阿达马设计，我们有：

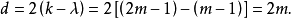因此，如果对于任意大的m存在维数m的阿达马设计，那么存在错误校正码，对于任意大的m，这个代码检测至多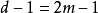个错误并校对至多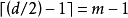个错误。这些代码是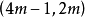代码，因为每一个代码字有长度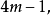我们称它们为阿达马码(Hadamardcode)2。

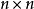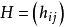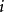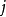构建阿达马设计的基本思想是，特定类型的矩阵给出这些设计的关联矩阵。一个矩阵被称为秩为n的阿达马矩阵(Hadamard matrix of order n)，如果对于每一个和有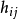等于+1或者等于-1，且如果

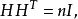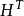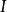其中是的转置矩阵，是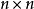单位矩阵。矩阵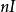在对角线下方为n，其余位置为。

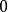一个阿达马矩阵称为是规范的(nomalized)，如果它的第一行和第一列只由十1组成，例如，矩阵

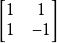是规范阿达马矩阵。而矩阵

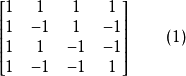也是规范阿达马矩阵。

阿达马矩阵的若干重要性质概括为如下定理。

定理2如果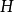是秩为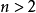的规范阿达马矩阵，那么对于某个m有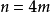，而且，除第一行(列)之外的每一行(列)正好有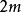个+1和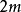个-1，而且对于除第一行(列)之外的任意两行(列)。都正好存在m列(行)，在这些列(行)上两行(列)都是+1。

这里，我们来看看定理2是如何给出定理1的证明的，给定一个规范阿达马矩阵，我们可以定义一个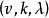设计。通过删除第一行和第一列，在其剩余部分，把每一个-1换成0就可以做到这一点正如我们将看到的那样，这样做给出一个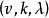设计的关联矩阵。在(1)式的阿达马矩阵上进行这一过程，首先给出

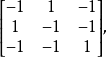于是这个关联矩阵是

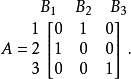这给出下面的区组：

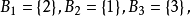而且产生一个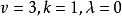的设计(从技术角度看，这不是一个设计，因为我们要求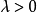然而，这可以说明该过程)。

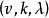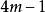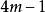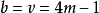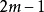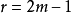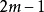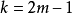为了证明这一过程总能给出设计，需要注意，根据定理2，关联矩阵A有个行和个列，所以，同样，从每一行消去一个1(第一个1)，所以A的每一行有个1，且,。通过类似的讨论，A的每一列有个1且。最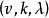后，任意两行在第一列上同时有两个1，所以现在同时有一个更少的对，即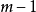对。所以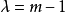，。因此，我们有设计，其中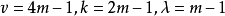且。

事实上，我们所描述的这一过程是可逆的，我们有下面的定理3。

定理3存在维数m的阿达马设计，与且仅当存在秩为4m的阿达马矩阵。

定理4如果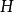是阿达马矩阵，那么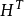也是阿达马矩阵2。