[科普中国]-混合张量

概念

混合张量(mixed tensor)是一类张量。向量空间及其对偶空间张量积的元素。张量空间：

(记为Vq)中的元素称为p重反变q重共变张量；或称为(p，q)重混合张量，其中V是C上向量空间，V*=L(V，C)是V的对偶空间。混合张量也指：

中的多重线性函数。可以定义张映射使：

V0中的元素称为反变张量。Vq中的元素称为共变张量。这些都是微分几何、黎曼几何及物理上用得较多的概念。1

张量张量是向量概念的综合，可用以代表各向量间的关系。例如弹性张量把弹性体上每一点的变形与外加应力联系起来。张量计算最初的发展是与微分几何相联系的，也是爱因斯坦在系统地阐述广义相对论时所用的基本工具。

n维空间中的一个量，它具有nr个分量，用表示，它的每个分量都是坐标的函数；在坐标变换下，这些分量按照一定的规律作线性变换。r称为张量的阶。

张量是矢量及矩阵概念的推广。标量是零阶张量;向量是一阶张量；矩阵是二阶张量。三阶张量(它的分量用Tijr表示)就像是一个“立体矩阵”。

在1900年，张量首先在弹性理论中使用。“张量”原来的含义是“张紧”与“张开”。

1892年起，里奇(C.G.Ricci，意，1853—1925)与列维·奇维塔(T.Levi-Civita，意，1873—1941)开始建立张量分析的理论，成为黎曼几何与广义相对论的一种工具。

为了简便，在张量列式或计算时，常按求和约定将求和号略去。

向量空间设K为交换体。称赋以由下列两个给定法则所定义的代数结构的集合E为K上的向量空间：

——记为加法的合成法则，

——记为乘法的作用法则，即从K×E到E中的映射，

这两个法则满足下列条件：

a)赋以加法的集合E是交换群；

b) 对K的任一元素偶(α，β)，以及对E的任一元素x，

c) 对E的任一向量x，1x=x，其中1表示体K的单位元素；

d)对K的任一元素偶(α，β)，以及对E的任一元素偶(x，y)，

当体K不再假定为交换的时，满足上述条件的集合E称为K上的左向量空间。

如果条件：α(βx)=(αβ)x换为：α(βx)=(βα)x，则称E为K上的右向量空间。在这种情况下，E上的作用法则记为：

例如，设K为交换体，而E为只有一个记为0的元素的集合。E赋以两个法则：

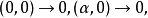则E为K上的向量空间。2

应用领域微分几何几何学的一门分支。主要以数学分析、微分方程为工具，研究光滑曲线，曲面在它一点邻域的性质。例如研究一般曲线和一般曲面在一点的曲率就是微分几何中的重要内容。近代由于对高维空间的微分几何和对曲线、曲面整体性质的研究，使微分几何与黎曼几何学、拓扑学、变分学、李群等有了密切的联系。上述各学科与微分几何的互相渗透已成为现代数学的中心问题之一。微分几何在力学和 一些工程问题(如弹性薄壳结构、齿论啮合理论等方面)中有广泛的应用。

黎曼几何黎曼几何是非欧几何的一种，亦称“椭圆几何”。德国数学家黎曼，对空间与几何的概念作了深入的研究，于1854年发表《论作为几何学基础的假设》一文，创立了黎曼几何。它与欧氏几何的主要区别，一是改变了欧氏几何的平行公理，规定通过某一点，不能引出一条直线与已知直线平行;二是证明三角形三内角和大于180°。黎曼假定所有的直线都是无界的，但其长度有限，也就是说，可以把直线看成是首尾相连，就象一个圆的圆周或球面上的大圆圆弧的情形那样，一个点沿一直线移动，最后将回到它的出发点上来。在黎曼所想象的空间里，过一点作一直线与另一直线平行是不可能的，平面上任何两条直线，只要延长到足够远就可以相交。黎曼几何在爱因斯坦创立广义相对论时，成为有力的数学工具。例如引力场附近的弯曲时空，就以黎曼几何为其数学基础。

非欧几何(罗氏几何、黎曼几何)的产生，突破了欧氏空间的唯一性。欧氏、罗氏和黎氏几何反映和揭示了空间形式的多样性，欧氏几何反映了曲率为零的平直空间，罗氏几何反映了曲率为负的弯曲空间，黎氏几何则反映了曲率为正数的弯曲空间，这些新发现使人们对空间性质的认识有了新的进展，可以说是人类对空间的认识史上的一次飞跃，而且扩展了几何学的应用范围。德国数学家希尔伯特曾说：“十九世纪最有启发性、最重要的数学成就是非欧几何的发现。”3