[科普中国]-对偶规划

发现简史

对偶规划最初是由冯·诺伊曼（vonNeu-mann，J.）于1947年提出来的，以后库恩（Kuhn，H.W.）和塔克尔(Tucker，A.W.）证明了对偶定理。哥德曼(Goldman，A.J.）和塔克尔于1956年比较系统地叙述了对偶规划的理论。

对偶线性规划的经济背景是：若原问题是利用有限资源安排最优生产方案，以获得最大总产值的线性规划问题，则它的对偶问题就是在相同资源的条件下，正确估计资源的使用价值，以达到支付最少费用的线性规划问题。简言之，若原问题为求解资源的最优配置问题，则对偶问题就是求解估价资源的使用价值问题。2

定律定义标准形式假定原问题是最大化问题，即线性规划问题（LP），它的标准形式：

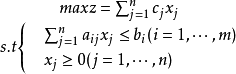
其对偶问题（DLP）如下式所示：3

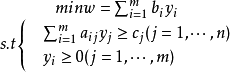
矩阵形式用矩阵形式表示，对称形式的线性规划问题的原问题为：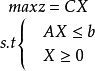

其对偶问题为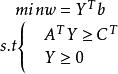： 或写作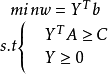

对偶问题转化一般形式上述都是一对对称形式的对偶线性规划，在原线性规划问题与对偶线性规划问题之间有着整齐的对称性，其特征是：

1.一个问题求极大max，对应另一个问题求极小min。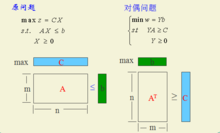

2.求极大问题中的约束条件为“≤”，求极小问题中的约束条件为“≥”。

3.原问题中有个变量，对偶问题中就有个约束条件。原问题中有m个约束条件，对偶问题中就有m个变量（称为对偶变量）。

4.原问题的目标函数中变量的系数就是对偶问题约束条件的常数项。原问题中约束条件的常数项就是对偶问题目标函数中变量的系数。

5.两个互为对偶问题的约束条件的系数矩阵互为转置矩阵。

6.原问题与对偶问题中的变量均有非负约束。4

非对称形式因为并非所有线性规划问题具有对称形式，故对下面讨论更加一般形式下线性规划问题如何写出其对偶问题。无论是堆成或非堆成的线性规划问题在写出其对偶问题时，对于A、B、C和目标函数的对应关系都适用，区别的只是约束条件的形式与其对应变量的取值。下面将对称或不对称线性规划原问题同对偶问题的转换时的对应关系，统一归纳为下表所示形式。

|| ||

性质对称性对称定理：对偶问题的对偶问题是原问题。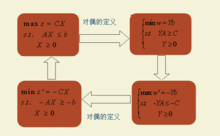

弱对偶性弱对偶性定理：Xo、Yo若分别是标准形式的原问题及对偶问题的可行解，则有CXo≤Yob。

最优性如果Xo是原问题的可行解，Yo是对偶问题的可行解，并且CXo=Yob，那么Xo和Yo分别为原问题和对偶问题的最优解。

对偶性对偶定理（强对偶性）：若原问题及其对偶问题均具有可行解，则两者均具有最优解，且它们最优解的目标函数值相等。

互补松弛性设Xo，Yo分别是原问题和对偶问题的可行解，Uo为原问题的松弛变量的值、Vo为对偶问题剩余变量的值。Xo, Yo分别是原问题和对偶问题最优解的充分必要条件是 YoUo = 0，VoXo= 0。5