备择假设
设总体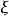 的分布函数
的分布函数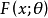 中,
中,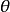 为未知参数,
为未知参数,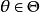 ,
,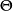 为参数空间。我们将参数空间
为参数空间。我们将参数空间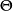 分解为互不相交的两个部分
分解为互不相交的两个部分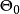 及
及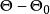 ,即
,即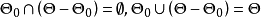 . 考虑检验问题:
. 考虑检验问题:
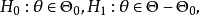
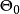 为非空子集,
为非空子集,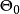 是假设检验的对象,称
是假设检验的对象,称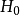 为原假设(或零假设),称
为原假设(或零假设),称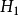 为备择假设(或备选假设,对立假设)。1
为备择假设(或备选假设,对立假设)。1
简单备择假设如果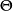 只含有两个点,即若
只含有两个点,即若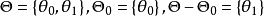 ,则有
,则有
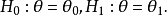 这时称
这时称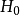 及
及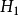 分别为简单原假设及简单备择假设。1
分别为简单原假设及简单备择假设。1
复合备择假设如果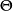 多于两个点,即若
多于两个点,即若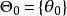 ,而
,而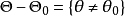 为非单点集,即有
为非单点集,即有
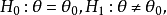 则称
则称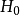 为简单原假设,
为简单原假设,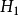 为复合备择假设。
为复合备择假设。
注:若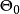 及
及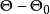 都是非单点集,则称
都是非单点集,则称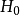 及
及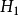 都是复合的。1
都是复合的。1
应用-检验法优劣的比较备择假设是原假设被否定时准备接受的假设,它是按少犯第二类错误(见下文)来比较检验法优劣时必不可少的。下面做详细阐述。
检验的功效原假设的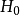 实际的“真伪”是不知道的,是不可观测的。人们通过一定的检验法基于样本对其“真伪”作出判断,称为统计推断。客观上,存在下面4种情况。
实际的“真伪”是不知道的,是不可观测的。人们通过一定的检验法基于样本对其“真伪”作出判断,称为统计推断。客观上,存在下面4种情况。
(1)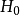 为真,统计推断是拒绝
为真,统计推断是拒绝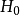 ;(犯第一类错误,也称“弃真错误”)
;(犯第一类错误,也称“弃真错误”)
(2)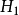 为真,统计推断是接受
为真,统计推断是接受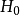 ;(犯第二类错误,也称“取伪错误”)
;(犯第二类错误,也称“取伪错误”)
(3)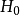 为真,统计推断是接受
为真,统计推断是接受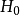 ;(推断正确)
;(推断正确)
(4)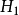 为真,统计推断是拒绝
为真,统计推断是拒绝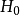 ;(推断正确)
;(推断正确)
情况(4)的概率称为检验的功效。显然,检验的功效=1-犯第二类错误的概率。1
比较检验法优劣的原则一个好的检验法应该尽可能得减小犯两种错误的概率,但同时减小犯两种错误的概率往往难以做到。故通常的做法是:控制犯第一类错误的概率,使犯第二类错误的概率尽可能地小(也可以说使检验的功效尽可能地大)。1
一致最优功效检验(UMPT)依据上述比较原则,在检验水平为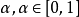 的检验(相当于控制了犯第一类错误的概率)中,功效最大者(相当于犯第二类错误的概率最小者)称为水平为
的检验(相当于控制了犯第一类错误的概率)中,功效最大者(相当于犯第二类错误的概率最小者)称为水平为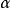 的一致最优功效检验,简记为UMPT(Uniformly Most Powerful Test)。1
的一致最优功效检验,简记为UMPT(Uniformly Most Powerful Test)。1
备择假设的选取由于假设检验的基本原理为:在一次试验中,小概率事件不易发生(或几乎不可能发生),因此,我们在确立原假设与备择假设时应遵循以下两个原则:
(1)原假设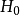 是在一次试验中有绝对优势出现的事件,而备择假设
是在一次试验中有绝对优势出现的事件,而备择假设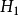 在一次试验中不易发生(或几乎不可能发生)的事件。 因此,在进行单侧检验时,最好把原假设
在一次试验中不易发生(或几乎不可能发生)的事件。 因此,在进行单侧检验时,最好把原假设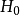 取为预想结果的反面,即把希望证明的命题放在备择假设上。
取为预想结果的反面,即把希望证明的命题放在备择假设上。
(2)将可能犯的严重错误看作第一类错误,因为犯第一类错误的概率可以控制, 犯第二类错误的概率是无法控制的。 如医生对前来问诊的病人作诊断时,可能会犯“有病看成无病”或者“无病看成有病”的错误,相比较而言,“有病看成无病”的错误更严重,故应将“问诊人有病”作为原假设。 而在某项疾病普查中,将“被检查人无病”作为原假设就不恰当了。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国