定义
设R是集合A上的关系,称集合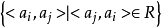 是R的逆关系,记作
是R的逆关系,记作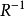 ,符号
,符号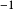 称为关系的求逆运算符。
称为关系的求逆运算符。
例如实数集合上的“大于等于”关系和“小于等于”关系。整数集合上的“整除”关系和“被整除”关系,幂集合上的“包含”关系和“被包含”关系,均互为逆关系,有些关系的逆关系是它自己。例如整数集合上的模k同余关系和幂集上集合的补关系的逆关系是它自己2。
相关定理定理1若R是集合A上的关系,则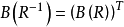 。2
。2
**证明:**仅需证明:对于任意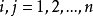 ,有
,有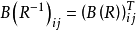 ,
,
若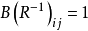 ,则
,则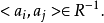 ;
;
因此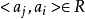 ;
;
因此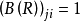 ;
;
所以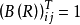 ;
;
若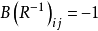 ,则
,则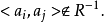 ;
;
因此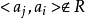 ;
;
因此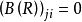 ;
;
所以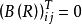 ;
;
综上,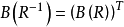 。
。
定理2若集合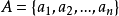 ,
,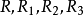 都是集合A上的关系,则有
都是集合A上的关系,则有
(1) 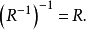
(2) 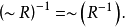
(3) 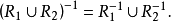
(4) 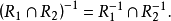
(5) 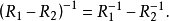 2
2
仅需证明:对于任意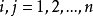 ,
,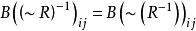 成立。
成立。
根据关系代数和布尔矩阵代数的同构性质,有
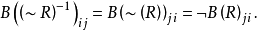
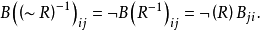 因此可得
因此可得
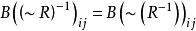
例题解析设集合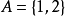 ,R和S均为A上的二元关系,且
,R和S均为A上的二元关系,且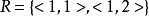 ,
,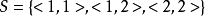 ,且
,且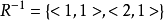 ,
,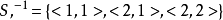 ,可见
,可见
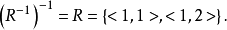
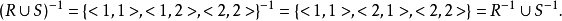
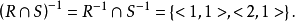
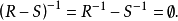




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国