历史
傅里叶展开式是一个函数的傅里叶级数在它收敛于此函数本身时的一种称呼。而傅里叶级数得名于法国数学家约瑟夫·傅里叶(1768年–1830年),他提出任何函数都可以展开为三角级数。此前数学家如拉格朗日等已经找到了一些非周期函数的三角级数展开,而认定一个函数有三角级数展开之后,通过积分方法计算其系数的公式,欧拉、达朗贝尔和克莱罗早已发现,傅里叶的工作得到了丹尼尔·伯努利的赞助。傅里叶介入三角级数用来解热传导方程,其最初论文在1807年经拉格朗日、拉普拉斯和勒让德评审后被拒绝出版,他目前被称为傅里叶逆转定理的理论后来发表于1820年的《热的解析理论》中。将周期函数分解为简单振荡函数的总和的最早想法,可以追溯至公元前3世纪古代天文学家的均轮和本轮学说。
傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。
定义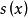 表示实变量
表示实变量 的一个函数,且
的一个函数,且 在
在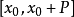 上可积,
上可积,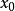 和
和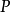 为实数。我们将尝试用谐波关系的正弦函数的无穷和或级数来表示该区间内的
为实数。我们将尝试用谐波关系的正弦函数的无穷和或级数来表示该区间内的 。在区间外,级数以
。在区间外,级数以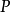 为周期(频率为
为周期(频率为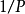 )。若
)。若 也具有该性质,则它的近似在整个实数线上有效。我们可以从有限求和(或部分和)开始1:
也具有该性质,则它的近似在整个实数线上有效。我们可以从有限求和(或部分和)开始1:

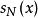 为周期为
为周期为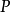 的周期函数。运用恒等式:
的周期函数。运用恒等式:
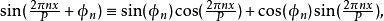
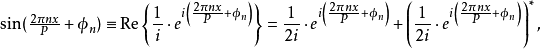
我们还可以用这些等价形式书写这个函数:
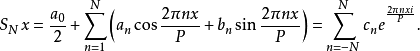 其中:
其中:
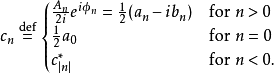
当系数(即傅里叶系数)以下面方式计算时:
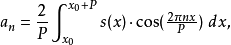
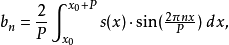
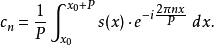
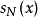 在
在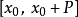 近似了
近似了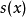 ,该近似程度会随着N→∞ 逐渐改善。这个无穷和
,该近似程度会随着N→∞ 逐渐改善。这个无穷和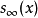 叫做
叫做 的傅里叶级数。在工程应用中,一般假定傅里叶级数除了在不连续点以外处处收敛,原因是工程上遇到的函数比数学家提供的这个假定的反例表现更加良好。特别地,傅里叶级数绝对收敛且一致收敛于s(x),只要在s(x) 的导数(或许不会处处存在)是平方可积的。 如果一个函数在区间 [x0, x0+P]上是平方可积的,那么此傅里叶级数在几乎所有点都收敛于该函数。傅里叶级数的收敛性取决于函数有限数量的极大值和极小值,这就是通常称为傅里叶级数的狄利克雷条件。参见傅里叶级数的收敛性之一。对于广义函数或分布也可以用范数或弱收敛定义傅里叶系数。
的傅里叶级数。在工程应用中,一般假定傅里叶级数除了在不连续点以外处处收敛,原因是工程上遇到的函数比数学家提供的这个假定的反例表现更加良好。特别地,傅里叶级数绝对收敛且一致收敛于s(x),只要在s(x) 的导数(或许不会处处存在)是平方可积的。 如果一个函数在区间 [x0, x0+P]上是平方可积的,那么此傅里叶级数在几乎所有点都收敛于该函数。傅里叶级数的收敛性取决于函数有限数量的极大值和极小值,这就是通常称为傅里叶级数的狄利克雷条件。参见傅里叶级数的收敛性之一。对于广义函数或分布也可以用范数或弱收敛定义傅里叶系数。
分类1.三角形式傅里叶展开式设周期信号f(t),其周期为T,角频率为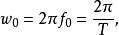 ,则该信号可展开为下面三角形式的傅里叶级数:
,则该信号可展开为下面三角形式的傅里叶级数:
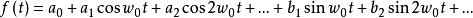
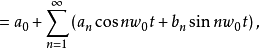
2.复指数形式傅里展开式设周期信号f(t),其周期为T,角频率为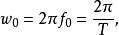 ,则该信号复指数的傅里叶级数:
,则该信号复指数的傅里叶级数:
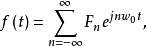
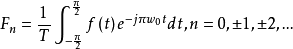
三角形式的傅里叶级数物理含义明确,而指数形式的傅里叶级数数学处理方便,而且很容易与后面介绍的傅里叶变换统一起来。两种形式的傅里叶级数的关系可由下式表示2:

收敛性判别至今还没有判断傅里叶级数的收敛性充分必要条件,但是对于实际问题中出现的函数,有很多种判别条件可用于判断收敛性。比如x(t)的可微性或级数的一致收敛性。在闭区间上满足狄利克雷条件的函数表示成的傅里叶级数都收敛。狄利克雷条件如下:
在定义区间上,x(t)须绝对可积;
在任一有限区间中,x(t)只能取有限个极值点;
在任何有限区间上,x(t)只能有有限个第一类间断点。
满足以上条件的x(t)傅里叶级数都收敛,且:
1. 当t是x(t)的连续点时,级数收敛于x(t);
2. 当t是x(t)的间断点时,级数收敛于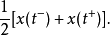
1966年,里纳特·卡尔松证明了勒贝格二次可积函数的傅立叶级数一定是几乎处处收敛的,即级数在除了一个勒贝格零测集外均收敛。
吉布斯现象:在x(t)的不可导点上,如果我们只取(1)式右边的无穷级数中的有限项作和X(t),那么X(t)在这些点上会有起伏。一个简单的例子是方波信号。
傅里叶展开式的意义**理论意义:**把复杂的周期函数用简单的三角级数表示;
**应用意义:**用三角函数之和近似表示复杂的周期函数。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国