[科普中国]-阿贝尔极限定理

阿贝尔极限定理是关于幂级数的和函数性质的重要定理之一，它断言：只要幂级数在其收敛区间的端点收敛，该级数的和函数就在该点（单侧）连续。

简介阿贝尔极限定理是关于幂级数的和函数性质的重要定理之一，它断言：只要幂级数在其收敛区间的端点收敛，该级数的和函数就在该点（单侧）连续。

阿贝尔极限定理说明，幂级数的和函数在该级数的收敛域上处处是连续的。1

幂级数幂级数，是数学分析当中重要概念之一，是指在级数的每一项均为与级数项序号 n 相对应的以常数倍的（x-a）的n次方（n是从0开始计数的整数，a为常数）。

幂级数是数学分析中的重要概念，被作为基础内容应用到了实变函数、复变函数等众多领域当中。

幂级数的和函数的性质性质一：幂级数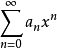的和函数s（x）在其收敛域I上连续。

性质二：幂级数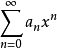的和函数s（x）在其收敛域I上可积，并有逐项积分公式

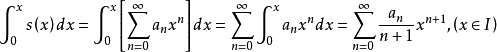
逐项积分后所得的幂级数和原级数有相同的收敛半径。

推论：幂级数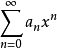的和函数s（x）在其收敛域内可逐项积分任意次。

性质三：幂级数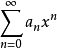的和函数s（x）在其收敛区间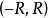内可导，并有逐项求导公式

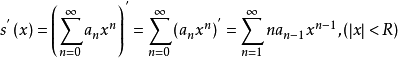
逐项求导后所得的幂级数和原级数有相同的收敛半径。

推论：幂级数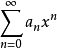的和函数s（x）在其收敛区间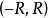内有任意阶导数。

本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学