逐项微分(term by term differentiation)是微积分术语,即函数列(级数)各项先求导数后求极限与极限(和)的导数相等,对函数列(级数)的每一项求导数,使所得到的序列(级数)收敛于原序列(级数)的极限(和)的导数。
基本介绍逐项微分是微积分术语,即函数列(级数)各项先求导数后求极限与极限(和)的导数相等,对函数列(级数)的每一项求导数,使所得到的序列(级数)收敛于原序列(级数)的极限(和)的导数,即
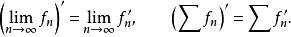
逐项微分有如下定理:若在区间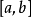 上
上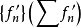 一致收敛,且
一致收敛,且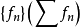 在
在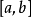 的某个点收敛,则
的某个点收敛,则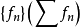 在
在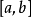 上一致收敛且可逐项微分,当
上一致收敛且可逐项微分,当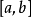 换成开集或任意区间
换成开集或任意区间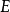 时,第一个条件可换成在
时,第一个条件可换成在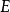 的任何闭子区间上一致收敛。特别地,幂级数在其收敛区间上可逐项微分任意次,并且每次得到的级数的收敛半径均相等1。
的任何闭子区间上一致收敛。特别地,幂级数在其收敛区间上可逐项微分任意次,并且每次得到的级数的收敛半径均相等1。
富比尼逐项微分定理富比尼逐项微分定理(Fubini term by term differential theorem)是有关级数逐项微分的定理,若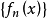 是区间
是区间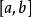 上一列不减(或不增)的函数,使得
上一列不减(或不增)的函数,使得
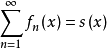 在
在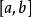 上处处存在且有限,则
上处处存在且有限,则
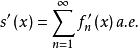 于
于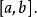
这是由富比尼(G.Fubini,)于1915年得到的,此定理中的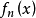 的条件明显可改为增函数之和,但不可改为增函数之差(有界变差函数)1。
的条件明显可改为增函数之和,但不可改为增函数之差(有界变差函数)1。
傅里叶级数的逐项微分傅里叶级数的逐项微分(term by term differentiation for Fourier series)是傅里叶级数的一种运算。若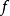 是以
是以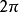 为周期的连续函数且除有限个点外可微,又导函数
为周期的连续函数且除有限个点外可微,又导函数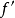 在
在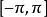 上可积,则
上可积,则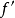 的傅里叶级数可由
的傅里叶级数可由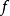 的傅里叶级数逐项微分得到,即若
的傅里叶级数逐项微分得到,即若
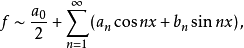 则
则
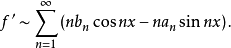 若
若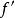 分段可微,则逐项微分后的级数收敛,且1
分段可微,则逐项微分后的级数收敛,且1
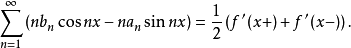
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国