定义
若任意数项级数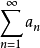 的各项的绝对值组成的级数
的各项的绝对值组成的级数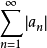 是收敛的,则称级数
是收敛的,则称级数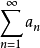 是绝对收敛级数。1
是绝对收敛级数。1
性质1)绝对收敛的级数是收敛的,但是,收敛的级数不一定是绝对收敛的(非绝对收敛的收敛级数称为条件收敛级数);2
2)若级数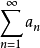 绝对收敛,则任意交换它的各项顺序后所得的新级数也绝对收敛,且其和不变;
绝对收敛,则任意交换它的各项顺序后所得的新级数也绝对收敛,且其和不变;
3)若级数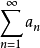 和
和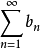 都绝对收敛,其和分别为A与B,则级数
都绝对收敛,其和分别为A与B,则级数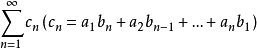 也绝对收敛,其和等于AB。3
也绝对收敛,其和等于AB。3
判别法1)比较判别法
设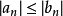 ,
,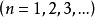
①若级数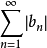 收敛,则级数
收敛,则级数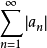 也收敛,即
也收敛,即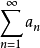 绝对收敛;
绝对收敛;
②若级数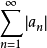 发散,则级数
发散,则级数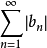 也发散,即
也发散,即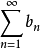 非绝对收敛。
非绝对收敛。
2)比较判别法的极限形式
设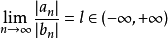
①若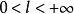 ,则级数
,则级数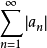 与级数
与级数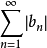 同时敛散;
同时敛散;
②若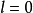 ,则级数
,则级数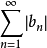 收敛时,级数
收敛时,级数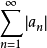 也收敛;
也收敛;
③若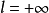 ,则当级数
,则当级数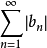 发散时,级数
发散时,级数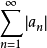 也发散。
也发散。
3)比值判别法
设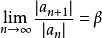
①当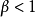 时,级数
时,级数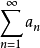 绝对收敛;
绝对收敛;
②当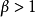 时,级数
时,级数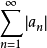 发散,级数
发散,级数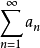 也发散。特别地,当
也发散。特别地,当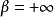 时,级数
时,级数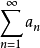 发散;
发散;
③当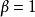 时,比值判别法失效(即无法通过比值判别法判断级数是否绝对收敛)。
时,比值判别法失效(即无法通过比值判别法判断级数是否绝对收敛)。
4)Raabe判别法
设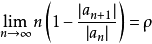
①当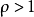 时,级数
时,级数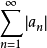 收敛;
收敛;
②当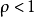 时,级数
时,级数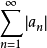 发散。4
发散。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国