基本介绍
设空间有界曲面 为
为
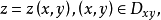 其中
其中 是
是 在
在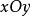 面上的投影区域,
面上的投影区域, 在
在 上具有连续的偏导数,下面讨论曲面
上具有连续的偏导数,下面讨论曲面 的面积的计算问题。
的面积的计算问题。
现用平行于x轴和y轴的两组平行直线分割投影区域 ,如图1所示,任取其中的一块记作
,如图1所示,任取其中的一块记作 ,其面积也记作
,其面积也记作 ,则当
,则当 的直径很小时,
的直径很小时,
 表示以
表示以 的边界为准线,母线平行于z轴的柱面截得的曲面
的边界为准线,母线平行于z轴的柱面截得的曲面 上的那部分,设
上的那部分,设 是
是 上的任一点,根据条件,曲面
上的任一点,根据条件,曲面 在点P处有切平面,则可用柱面截得切平面上的那一小片平面的面积dS近似地代替
在点P处有切平面,则可用柱面截得切平面上的那一小片平面的面积dS近似地代替 的面积
的面积 ,则
,则
 其中,
其中, 是切平面与
是切平面与 面的夹角,也就是切平面的法向量n与
面的夹角,也就是切平面的法向量n与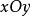 面的法线
面的法线 轴的夹角,由曲面
轴的夹角,由曲面 的方程可知
的方程可知
 所以
所以
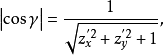 代人式(1)得
代人式(1)得
 则曲面的面积微元为
则曲面的面积微元为
 将dS在投影区域
将dS在投影区域 上积分,便得计算曲面面积的二重积分公式
上积分,便得计算曲面面积的二重积分公式
 如果所求曲面的方程用
如果所求曲面的方程用 或
或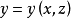 表示比较方便,则同理可将曲面分别投影到
表示比较方便,则同理可将曲面分别投影到 面或
面或 面,类似地可得相应曲面的面积计算公式,分别为
面,类似地可得相应曲面的面积计算公式,分别为
 或
或
 其中,
其中,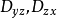 分别为曲面
分别为曲面 在yOz面或zOx面上的投影区域。1
在yOz面或zOx面上的投影区域。1
例题解析例1 证明球面 的表面积为
的表面积为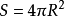 。
。
解: 由对称性,取上半球面方程为 ,它在xOy面上的投影区域为
,它在xOy面上的投影区域为

 由式(2)得
由式(2)得
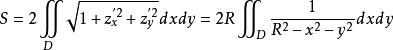

例2 求抛物面 位于
位于 之间的那一部分的面积。1
之间的那一部分的面积。1
解: 曲面在xOy面上的投影区域 ,由式(2),得
,由式(2),得






 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国