设a,b是两个整数,其中b>0,则存在两个唯一的整数q及r,使得a=bq+r,0≤r0,在不致引起混淆的情况下,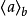 中的b常略去不写1。
中的b常略去不写1。
相关性质非负最小剩余有下面的性质(各式中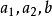 都是整数,且b>0,b略去未写):
都是整数,且b>0,b略去未写):
1.两个整数和的非负最小剩余,等于这两个整数各自的非负最小剩余的和的非负最小剩余,即
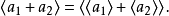
2.两个整数差的非负最小剩余,等于这两个整数各自的非负最小剩余的差的非负最小剩余,即
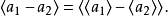
3.两个整数积的非负最小剩余,等于这两个整数各自的非负最小剩余的积的非负最小剩余,即1
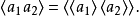
相关概念同余式在整数与它们被一个已知的正整数m除的余数的关系中来讨论同余式,m叫做模。
如果与两个整数 和b对应的是同一个余数r,则它们就被叫做对于模m同余。
和b对应的是同一个余数r,则它们就被叫做对于模m同余。
对于模m同余的数 和b写成
和b写成
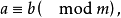 而且读做:对于模m,
而且读做:对于模m, 与b同余。
与b同余。
数 和b对于模m的同余性,等价于:
和b对于模m的同余性,等价于:
1. 可以表成
可以表成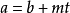 ,这里
,这里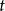 是整数。
是整数。
2.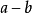 被m除尽。
被m除尽。
完全剩余组a.对于模m同余的数组成由模m决定的数类。
从这个定义知道,与同一个类的所有数对应的是同一个余数 ,而且只要在式子
,而且只要在式子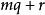 里让q通过所有的整数,我们就得到这个类里的所有数。
里让q通过所有的整数,我们就得到这个类里的所有数。
对应于 的m个不同的值,我们有m个由模m决定的数类。
的m个不同的值,我们有m个由模m决定的数类。
b.一个类的任意数,对于同一个类的所有数而言,都叫做模m的剩余,当q=0时,我们得到的剩余正好等于余数 ,叫做非负的最小剩余。
,叫做非负的最小剩余。
按绝对值说最小的剩余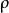 叫做绝对的最小剩余。
叫做绝对的最小剩余。
c.对于模m两两不同余的任意m个数,组成这个模的完全剩余组。
实际上,由于不同余的缘故,这些数属于不同的类,而因它们的个数m正好是类的个数,所以在每个类里正好有一个数。
d.如果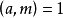 ,而且
,而且 通过模m的完全剩余组,则
通过模m的完全剩余组,则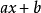 (b是任意整数)也通过模m的完全剩余组2。
(b是任意整数)也通过模m的完全剩余组2。
与模互素的剩余组a.模m的同一个类里的数与模有同一个最大公约数。特别重要的是这个公约数等于1的类,即包含着与模互素的数的类。
从每个这样的类取一个剩余,我们得到与模m互素的剩余组。因此,可以取完全剩余组里与模互素的数来组成与模互素的剩余组。通常与模互素的剩余组从非负的最小剩余组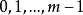 中分出。因为在这m个数中间,与m互素的有
中分出。因为在这m个数中间,与m互素的有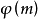 个,所以与模互素的剩余组里数的个数,即包含与模互素的数的类的个数,是
个,所以与模互素的剩余组里数的个数,即包含与模互素的数的类的个数,是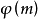 。
。
例子:与模42互素的剩余组是
1,5,11 ,13,17,19,23,25,29,31,37,41
b.对于模m两两不同余的任意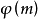 个与模互素的数,组成一个与模m互素的剩余组。
个与模互素的数,组成一个与模m互素的剩余组。
实际上,由于不同余而且与模互素的缘故,这些数属于不同的包含与模互素的数的类,而因为它们的个数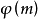 正好是这种样子的类的个数,所以在每个类里正好有一个数。
正好是这种样子的类的个数,所以在每个类里正好有一个数。
c.如果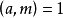 ,而且x通过与模m互素的剩余组,则ax也通过与模m互素的剩余组2。
,而且x通过与模m互素的剩余组,则ax也通过与模m互素的剩余组2。
欧拉定理和费马定理a.当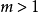 和
和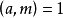 时,我们有(欧拉定理)
时,我们有(欧拉定理)
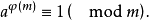
实际上,如果x通过从非负的最小剩余得来的与模互素的剩余组
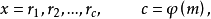 则ax的非负的最小剩余组
则ax的非负的最小剩余组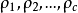 也是这样的组,只是一般说来次序有变动罢了。
也是这样的组,只是一般说来次序有变动罢了。
b.当p是素数而且 不被p除尽时,我们有(费马( Fermat)定理)
不被p除尽时,我们有(费马( Fermat)定理)
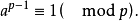 这定理是定理a当m=p时的推论,这个定理可以给予更便利的形式,那就是说,在上述同余式两边乘上a,我们得到同余式
这定理是定理a当m=p时的推论,这个定理可以给予更便利的形式,那就是说,在上述同余式两边乘上a,我们得到同余式
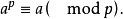 它对于所有的整数a都正确,因为当a是p的倍数时它也成立2。
它对于所有的整数a都正确,因为当a是p的倍数时它也成立2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国