[科普中国]-双曲面渐近锥面

双曲面的渐近锥面(asymptotic conical surface of hyperboloid)是刻画双曲面形状的锥面，由经过双曲面中心的双曲面的渐近线所组成的锥面。双曲面族(x2/a2)+(y2/b2)-(z2/c2)=K(参数K≠0)有共同的渐近锥面(x2/a2)+(y2/b2)-(z2/c2)=01。

基本介绍双曲面(hyperboloid(surface))是指在通过主轴的平面上，截痕是双曲线，而在与主轴垂直的平面上的截痕是椭圆的二次曲面。它分为单叶双曲面和双叶双曲面，它们都关于三个相互垂直的平面中每一个平面对称。

在平面几何中，双曲线有渐近线，相类似地，双曲面也有渐近锥面。二次锥面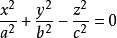是单叶双曲面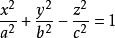和双叶双曲面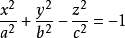的渐近锥面2。

二次锥面是双曲面的渐近锥面现在我们来考虑单叶双曲面(1)和双叶双曲面(2)与二次锥面(3)。

单叶双曲面

双叶双曲面

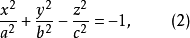
二次锥面

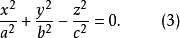
当它们有相同的正数a，b，c时，则它们有密切的关系。

用平行于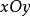坐标面的平面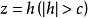去截三个曲面。所得截线方程为

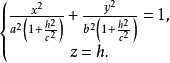
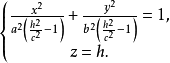和

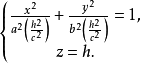它们都是椭圆，具有相同的中心和对称轴，并且曲面对应的半轴分别为

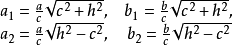和

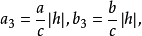但它们的半轴的比相等

所以在平面z=h上截线椭圆的形状相似，很明显有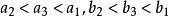。但当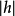无限增大时，差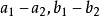趋于零。事实上

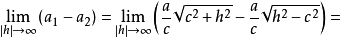
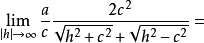
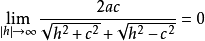同理得

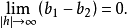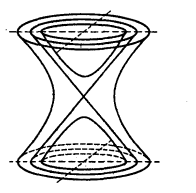
可见，当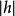无限增大时，三个曲面无限接近。即单叶双曲面和双叶双曲面都与二次锥面(3)无限接近，我们称二次锥面(3)是双曲面(1)和(2)的渐近锥面(图1)2。

例题解析**【例1】** 用一族平行平面z=h(h为参数)截割单叶双曲面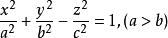得一族椭圆，求这些椭圆焦点的轨迹。

**解：**所截得的椭圆族方程为

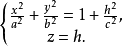即

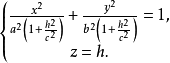因为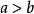，所以椭圆的长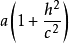半轴为，短半轴为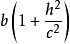，从而椭圆焦点的坐标为

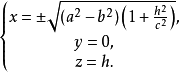消去参数h得

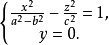显然这族椭圆焦点的轨迹是一条在坐标面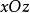上的双曲线。双曲线的实轴为x轴，虚轴为z轴2。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学