[科普中国]-集中趋势量数

集中趋势的统计量

一维资料的集中趋势可能有以下数种统计方法。在某些情况下，经转型（data transformation）后的资料才采用以下的方法。

算数平均数观测值的总和除以观测值的个数，即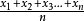 。常简称为平均数，也往往是背后机率分布的期望值之不偏估计。

中位数将所有观测值按大小排序后在顺序上居中的数值。

众数出现最多次的观测值。

几何平均数观测值的乘积之观测值个数方根，即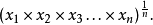

调和平均数观测值个数除以观测值倒数的总和，即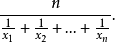

加权平均数考虑不同群资料贡献程度不同时的算数平均数。

截尾平均数（truncated mean）忽略特定比例或特定数值之外的极端值后所得的平均数。例如，四分平均数（interquartile mean）正是忽略25%前及75%后的资料后所得的算数平均数。

全距中点（midrange）最大值与最小值的算数平均数，即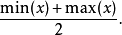

中枢纽（midhinge）第一四分位数与第三四分位数的算数平均数，即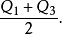

三均值（trimean）考虑三个四分位数的加权平均数，即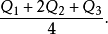

极端值调整平均数（winsorized mean）以最接近的观测值取代特定比例的极端值后取得的算数平均数。举例来说，考虑10个观测值（由小到大排列为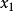至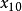）的情况下，10%的极端值调整平均数为

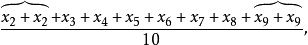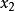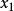其中分别以和取代了和。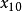

以上的统计量在多维变数中仍可单独地被套用在各个维度上进行，但并不能保证在转轴后仍维持一致的结果。12

平均数、中位数与众数的关系在左右对称的机率分布中，不同的集中趋势统计量有相同结果，但在偏度远离0时则可能不一致。在单峰型的机率分布（unimodal probability distribution）中，平均数（μ）、中位数（ν）与众数（θ）的关系如下：

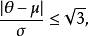
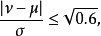
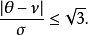其中σ为标准偏差。至于任一机率分布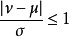，。3