[科普中国]-总体均值

总体均值(population mean)又叫做总体的数学期望或简称期望，是描述随机变量取值平均状况的数字特征。包括离散型随机变量的总体均值：和连续型随机变量的总体均值。

基本介绍总体均值又叫做总体的数学期望或简称期望，是描述随机变量取值平均状况的数字特征1。

离散型随机变量的总体均值设离散型随机变量 的可能取值是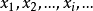 ，取这些值的相应概率为

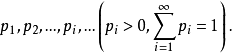
若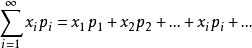 绝对收敛，则 称为随机变量的总体均值。记作

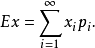
连续型随机变量的总体均值设连续型随机变量 的分布密度是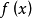 ，若积分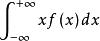 绝对收敛，则称该积分为总体 的均值，记作 。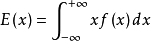

总体均值的基本性质总体均值具有以下基本性质：

①对任意常数c，均有 ；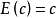

②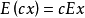 ，其中c为任意常数；

③ ，其中c为任意常数；

④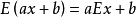 ，其中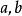 为任意常数；

⑤对于两个随机变量x和y，有 ；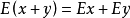

⑥若两个随机变量x和y相互独立，则有 。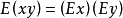

基本性质⑤、⑥可以推广到有限个的情况，这就是：n个随机变量和的均值等于均值的和；n个随机变量若相互独立，则乘积的均值等于均值的乘积。这时n为有限整数且大于21。

总体均值的点估计参数估计就是以样本统计量来估计总体参数，例如，用样本平均数估计总体平均数，用样本成数估计总体成数，等等。在参数估计中，用来估计总体参数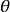 的样本统计量 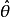，称为估计量。例如，样本平均数、样本成数、样本方差等。用来估计总体参数时计算出来的估计量的具体数值 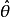，称为估计值。例如，要估计一个班级考试的平均分数，现从中抽取一个随机样本，经过计算得到样本平均分数为80分，那么这个80分就是估计值。

参数估计的方法有点估计和区间估计。

点估计就是直接以样本统计量作为总体参数的估计量，又称为定值估计。例如，以样本平均数、样本成数、样本方差作为相应总体参数的估计量，即

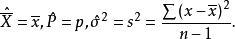
总体均值的区间估计方差已知时总体均值的区间估计若总体服从正态分布，则样本均值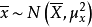 ；若总体不服从正态分布，但当样本容量n足够大时，则 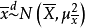。进一步可得2：

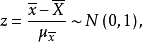给定显著性水平 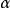，查标准正态分布表可得到临界值 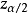，且满足：

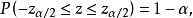则在置信水平 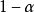下总体均值的区间估计为

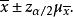反过来，设总体均值的抽样允许误差为 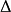，即 ，且区间估计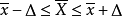 的置信水平为 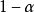，则有

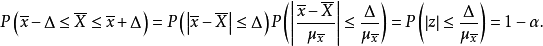
临界值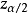 与置信水平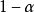 一一对应。给定一个置信水平 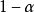，可以通过查标准正态****分布表确定临界值 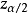。若置信水平提高，即区间估计的可靠程度增大，则 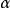减小，即临界值 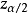增大。反之，若置信水平减小，则临界值减小。临界值 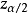称为概率度，用符号z表示，用以间接地衡量区间估计的概率大小。

易见，抽样允许误差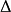 、抽样平均误差 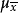和概率度z三者存在如下关系：

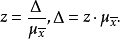
给定置信水平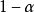 ，在重复抽样条件下，总体均值的置信区间为

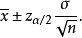
在不重复抽样条件下，总体均值的置信区间为

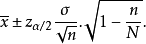
方差未知时总体均值的区间估计若总体服从正态分布但总体方差未知，则可用样本标准差s代替总体标准差s构造统计量，即得

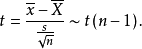
给定置信水平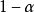 ，在重复抽样条件下，总体均值的置信区间为

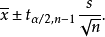
类似地，在不重复抽样条件下，总体均值的置信区间为

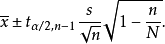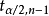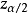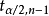查t分布表可得到临界值 。在大样本情况下，t分布近似于标准正态分布。所以，此时也可以用标准正态分布临界值 代替 2。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学