球面半边公式(formulas of the spherical half side)是球面三角的基本公式之一,即用与球面三角形各角有关的三角函数表示其各边之半的三角函数的公式1。
球面半边正弦公式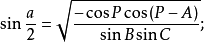
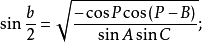
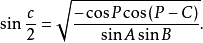
球面半边余弦公式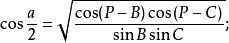
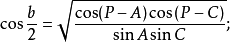
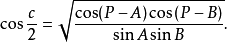
球面半边正切公式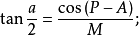
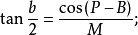
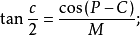

或:

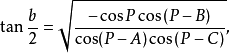
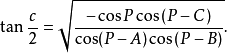
半边正弦公式的证明设球面三角形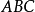 ,如图1,作球心三角形
,如图1,作球心三角形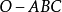 ,从球面三角形的任意一个顶点A向平面
,从球面三角形的任意一个顶点A向平面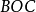 作垂线
作垂线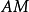 ,通过垂足
,通过垂足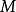 ,在平面
,在平面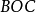 内作
内作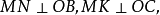 显然,
显然,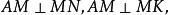 连接
连接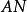 及
及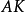 。
。
角的余弦公式:
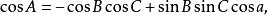
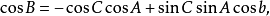
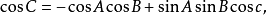
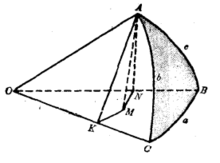
将图1中 平面上割点的相对位置用图2表示。
平面上割点的相对位置用图2表示。
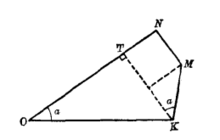
为了找出一边和三角的关系,我们利用角的余弦公式:
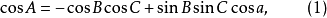 或
或
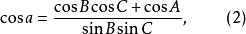 将它代入平面三角公式
将它代入平面三角公式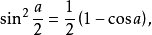 就得
就得
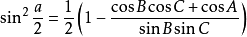
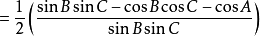
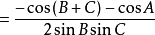 (和角公式)
(和角公式)
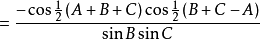 (和差化积公式).
(和差化积公式).
若令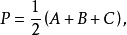 则
则
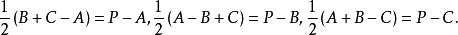 于是得:
于是得:
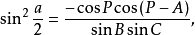 或:
或:
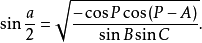 同理:
同理:
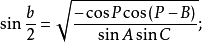
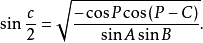
这就是半边正弦公式2。
半边余弦公式的证明若将(2)代入平面三角公式
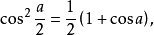 则仿照半边正弦公式的证明方法,可得半边余弦公式2:
则仿照半边正弦公式的证明方法,可得半边余弦公式2:
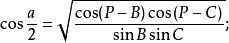
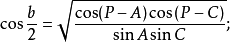
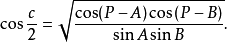
半边正切公式的证明将半边正弦公式和半边余弦公式相除,就得半边正切公式2:

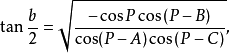
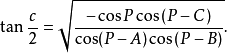
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国