指数中含有未知数的不等式叫指数不等式。指数不等式解法的主要思想是:根据不等式的基本性质,并利用指数函数和对数函数的单调性求得其解,或是转化为代数不等式再求解,至于稍复杂一些的指数不等式,是不可能用初等方法求解的。
基本介绍指数里含有未知数的不等式叫作指数不等式。
形如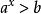 或
或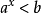 (
(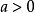 ,且
,且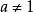 )的不等式叫作基本指数不等式或最简指数不等式。下列形式的每个不等式叫做初等指数不等式1:
)的不等式叫作基本指数不等式或最简指数不等式。下列形式的每个不等式叫做初等指数不等式1:
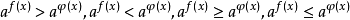 其中
其中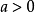 。还有形如
。还有形如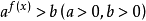 ,
,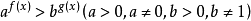 等的不等式也都是指数不等式。
等的不等式也都是指数不等式。
指数不等式的解法①形如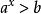 或
或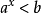 (
(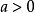 ,且
,且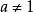 )的不等式的解法
)的不等式的解法
理论依据是指数函数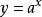 的单调性。
的单调性。
(1)当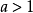 时,函数
时,函数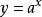 是增函数;
是增函数;
(2)当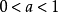 时,函数
时,函数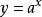 是减函数。
是减函数。
下面我们研究不等式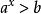 的解法:
的解法:
(1)当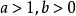 时,原不等式即为
时,原不等式即为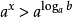 ,所以
,所以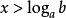 ;
;
(2)当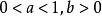 时,则有
时,则有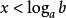 ;
;
(3)当 时,因
时,因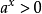 ,故
,故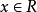 2。
2。
|| ||
②形如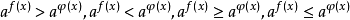 的解法
的解法
不等式: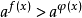 :
:
当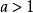 时等价于不等式1
时等价于不等式1
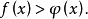
当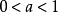 时等价于不等式
时等价于不等式

③ 形如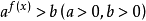 的解法
的解法
两边取常用对数:
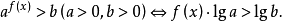
④形如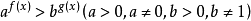
两边取常用对数:  。
。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国