[科普中国]-共轭直线

概念

共轭直线(conjugate lines)是指成对出现的两条直线。在射影空间中，给定一个非退化的二阶曲面∑，空间中每一点P都有一个确定的极面，对于空间中的一个点列，其对应的极面构成一个平面束，这个平面束的轴与点列的底称为关于二阶曲面∑的一对共轭直线。1

二阶曲面二阶曲面是空间射影几何研究的基本对象。设空间中点的齐次坐标或射影坐标为(x1，x2，x3，x4)，则满足四元二次齐次方程：

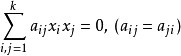的点的全体称为二阶曲面。这里aij为实数且至少一个不为零。该方程称为二阶曲面的方程。(aij)称为系数矩阵。若系数矩阵的行列式|aij|≠0，则二阶曲面称为非退化的，否则称其为退化的。在射影空间中，成射影对应的两个平面束对应平面的交线的轨迹是一个二阶曲面。

二次曲面在空间直角坐标系中，若方程 f(x，y，z)=0的左边是变量x，y，z的二次多项式，则它所代表的曲面叫做二次曲面。椭球面、抛物面、双曲面等都是二次曲面。

三维欧几里得空间里坐标x、y、z之间的二次方程：

ax2+by2+cz2+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0

(系数a，b，c，…为实数，二次项系数不全为零)表示的曲面。早在公元前3世纪，古希腊数学家阿基米德就写过一本《论球和圆柱》的论著，从几个定义和公理出发，推出关于球与圆柱的面积及体积等50多个命题。阿基米德、阿波罗尼奥斯、海伦等人还研究过抛物镜面的反射问题，这是早期对一些特殊二次曲面的探讨，其中被研究的还有双叶双曲面和椭球面，都是由圆锥截线绕轴旋转产生的曲面。

解析几何建立后，二次曲面研究在理论上有较大进展。1731年法国数学家克莱罗给出某些二次曲面的求积公式，并指出x、y、z的齐次方程表示顶点在原点的一个锥面。1748年大数学家欧拉在他的《无穷分析引论》中研究了三个变量的一般二次方程，得到6种二次曲面：锥面、柱面、椭球面、单叶和双叶双曲面、双曲抛物面以及抛物柱面，并主张按方程的次数将二次曲面进行分类，认为次数是线性变换下的不变量。1802年法国几何学家蒙日及其学生证明了二次曲面的每一个平面截口是一条二次曲线，且平行截面截得的是相似的二次曲线。1832年瑞士数学家施泰纳用射影几何的方法构造了直纹二次曲面理论，到今天已日臻完善，成为解析几何学的重要组成部分。

射影空间整体几何最基本的研究对象之一。射影空间的概念最初产生于古典射影几何。对于射影定理中的奇异情形(即有些直线相互平行的情形)，为方便起见引入无穷远点的概念，即规定平面上每条直线上有一个无穷远点，两条直线平行就是相交于无穷远点，所有无穷远点组成一条无穷远直线。这种构造方法还可以推广到高维空间，建立n维(实)射影空间PR。在n维射影空间中常采用齐次坐标(X0∶X1∶…∶Xn)，其中X0，X1，…，Xn不全为0；若a≠0，则(aX0∶aX1∶…∶aXn)与(X0∶X1∶…∶Xn)表示同一个点。因此n维(实)射影空间同构于(Rn+1-{0})/R。进一步的研究表明PR是紧致解析流形。若令Ui(0≤i≤n)为PR中坐标Xi≠0的点全体，则UiR，且U0，U1，…，Un组成PR的一个开覆盖。上述构造方法可以推广到任意体K上，建立K上的n维射影空间PK。在概形理论中，还将射影空间建立在整数环Z上，即建立射影概形PZ。由此对任意概形X可以建立PX，它是X和PZ(在Spec Z上)的纤维积。特别地，若X=Spec K(K为域)，则PX=PK。

由于射影空间的性质非常丰富难以全面列举，仅举数例如下：

1.P1R同胚于圆，P1C可看做添上无穷远点的复平面，同胚于球面。

2.P2R是单侧曲面，可以同胚地嵌入四维空间R4，但不能同胚地嵌入三维空间R3，P2C是代数极小曲面。

3.PnC是克勒流形，它的闭解析子空间都是代数的。

4.对任意域k，Pnk是齐性空间，其切丛由整体向量场生成，其自同构群为射影群PSL(n+1，k)，其皮卡群Pic(Pk)Z。2

共轭群中一种重要的等价关系。设S，T是群G的两个非空子集，H是G的子群，若存在H中元素g使得T=g-1Sg=Sg，则称S和T关于H共轭，其中T=g-1Sg={g1sg|s∈S}称为S按g的变形。若S为G的子群，T称为S关于H的共轭子群；若S={s}为一个元的集合，则称t=g-1sg为s关于H的共轭元。当H=G时，通常就不加“关于G”这个修饰词了。共轭关系是一种等价关系。设S是群G的一个子集，H是G的一个子群，与S关于H共轭的所有子集组成的集合称为S关于H的共轭类。当S={s}为一个元素的集合，s关于G的共轭类是元素的集合，就简称G(的元素)的一个共轭类。3