[科普中国]-有向球面三角形

有向球面三角形(directed spherical triangle)亦称定向球面三角形，是球面三角形的一种，指规定了三个顶点顺序的球面三角形。

基本介绍有向球面三角形亦称定向球面三角形，是球面三角形的一种，指规定了三个顶点顺序的球面三角形，有向球面三角形三个顶点的顺序，规定了球面三角形三条边的环行方向，这种环行方向有逆时针和顺时针两种(如图1)，通常取逆时针方向为正向，顶点顺序为正向的有向球面三角形称为正向球面三角形或正定向球面三角形；否则，称为负向球面三角形或负定向球面三角形。两个有向球面三角形在定向相同时称为同向球面三角形，定向相反时称为反向球面三角形，有向球面三角形的三个内角自然而成为定向协合的有向角1。

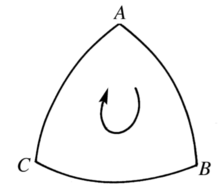
相关概念球面三角形将球面上的三个点用大圆弧连接起来所围成的图形称为球面三角形，这三个点称为球面三角形的顶点，三个大圆弧称为球面三角形的边，球面三角形的角就是三个大圆弧两两相交而成的球面角。

由于连接两点的大圆弧有两个不同弧段，将球面上三个点用三段大圆弧连接起来围成的图形方式一般有8种，如表1所示阴影部分和无阴影部分。因此，在一般情况下，由三个点规定的球面三角形共有8个，其中一个球面三角形的三个边都小于半个圆周，将这样的球面三角形称为简单球面三角****形，如图(a)中的阴影部分所示，简单球面三角形是经常用到的球面三角形2。

|| || 表1球面三角形

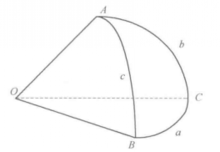
如下图所示，组成简单球面三角形的三个大圆弧所在平面构成一个三面角，其顶点为球心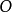，而其棱是由球心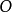到球面三角形三个顶点的半径。三面角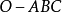的每一个平面角都可以用其相对的球面三角形的边来度量，而两个平面之间的夹角，即二面角等于其相应的球面三角形的球面角。

有向球面角有向球面角(oriented spherical angle)亦称定向球面角，球面几何的基本概念之一，即规定了始边和终边的球面角，同一球面上的所有有向球面角可按下列方式分为两类，设想观察者站在有向球面角的顶点处(人在球外)观察该有向球面角，这时必可发现下列两种情况之一：

1.从始边出发扫过角的内部旋转到终边的旋转方向是逆时针的；

2.从始边出发扫过角的内部旋转到终边的旋转方向是顺时针的。

通常规定逆时针方向是正方向，顺时针方向是负方向，上述第一种有向球面角称为正向球面角，第二种有向球面角称为负向球面角.对两个有向球面角，若它们的定向相同(即同为正向或同为负向)，则称它们是同向球面角；否则，称它们为反向球面角‘’1.

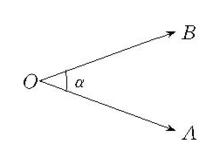
有向角有向角(directed angle)是三角学的基本概念之一。在平面几何中，角被理解为从一点引出的两条射线所组成的几何图形。如图2，角α是从O点引出的两条射线OA与OB组成的几何图形，角的概念是不断扩充的，从运动的观点出发，角被看做是一条射线在平面内绕其端点的旋转量，并规定：射线的初始位置称为角的始边;射线的终止位置称为角的终边；射线的端点称为角的顶点。引进上述概念后，就把角的始边绕其顶点扫过角的内部到与终边重合的旋转方向称为角的方向。因此，这种规定了方向的角就称为有向角，由于射线绕其端点的旋转，如拨动时针，所以有两个旋转方向。对于有向角，通常规定：始边按逆时针方向旋转所成的角为正角；始边按顺时针方向旋转所成的角为负角；始边未作旋转即与终边重合的角为零角。

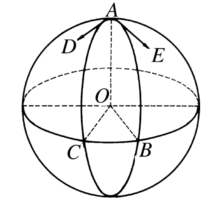
球面角球面角(spherical angle)是一种特殊的球面图形，指由球面上一点和以此点为公共端点的两条大圆弧所构成的球面图形，公共端点称为该球面角的顶点，两条大圆弧称为该球面角的边。若球面角的顶点是A，它的两条边分别通过点B，C(如图3)，则该球面角可以记为∠BAC或∠CAB，球面角的度量有以下三种方法：

1.用由平面AOC和AOB所构成的二面角来度量。

2.用以球面角顶点为极的大圆，被该球面角截得的大圆弧BC之长来度量。

3.用过顶点的两条边的切线所夹的角(平面角)∠DAE来度量。

球面角也可以定义锐角、直角或钝角，小于π/2的球面角称为锐球面角，等于π/2的球面角称为直球面角，大于π/2的球面角称为钝球面角1。

有向球面二角形球面二角形(spherical lune)亦称月形或瓜瓣形，是一种特殊的球面图形，球面上两个对径点和以这两点为端点的两个半大圆所围成的球面图形称为球面二角形，构成球面二角形的两个半大圆称为它的边，两个对径点称为它的顶点，一个顶点和两条边所构成的球面角称为它的角。

指规定了始边和终边的球面二角形叫有向球面二角形，对有向球面二角形两顶点所在的直线指定一个正方向，设想一观察者站在球面二角形的一个顶点处(其从脚到头的方向和上述指定的正方向一致)，观察该球面二角形从始边出发经球面二角形的内部到终边的旋转方向，这有两种可能的情形：

1.旋转方向是逆时针的；

2.旋转方向是顺时针的，

如果规定逆时针方向为正向，顺时针方向为负向，则凡从始边到终边的旋转方向是逆时针的球面二角形，称为正向球面二角形；否则，就称其为负向球面二角形1。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学