斜角球面三角形(oblique angled spherical triangle)是球面三角形的一种,指三个内角都不是直角的球面三角形。三个内角都是锐角的斜角球面三角形,称为锐角球面三角形;至少有一个内角是钝角的斜角球面三角形,称为钝角球面三角形1****。
基本介绍定义斜角球面三角形指三个内角都不是直角的球面三角形。三个内角都是锐角的斜角球面三角形,称为锐角球面三角形;至少有一个内角是钝角的斜角球面三角形,称为钝角球面三角形1。
球面三角形将球面上的三个点用大圆弧连接起来所围成的图形称为球面三角形,这三个点称为球面三角形的顶点,三个大圆弧称为球面三角形的边,球面三角形的角就是三个大圆弧两两相交而成的球面角。
由于连接两点的大圆弧有两个不同弧段,将球面上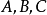 三个点用三段大圆弧连接起来围成的图形方式一般有8种,如表1所示阴影部分和无阴影部分。因此,在一般情况下,由三个点规定的球面三角形共有8个,其中一个球面三角形的三个边都小于半个圆周,将这样的球面三角形称为简单球面三角****形,如图(a)中的阴影部分所示,简单球面三角形是经常用到的球面三角形1。
三个点用三段大圆弧连接起来围成的图形方式一般有8种,如表1所示阴影部分和无阴影部分。因此,在一般情况下,由三个点规定的球面三角形共有8个,其中一个球面三角形的三个边都小于半个圆周,将这样的球面三角形称为简单球面三角****形,如图(a)中的阴影部分所示,简单球面三角形是经常用到的球面三角形1。
|| || 表1球面三角形
如下图所示,组成简单球面三角形的三个大圆弧所在平面构成一个三面角,其顶点为球心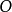 ,而其棱是由球心
,而其棱是由球心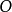 到球面三角形三个顶点
到球面三角形三个顶点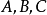 的半径。三面角
的半径。三面角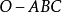 的每一个平面角都可以用其相对的球面三角形的边来度量,而两个平面之间的夹角,即二面角等于其相应的球面三角形的球面角。
的每一个平面角都可以用其相对的球面三角形的边来度量,而两个平面之间的夹角,即二面角等于其相应的球面三角形的球面角。
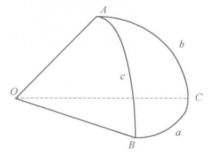
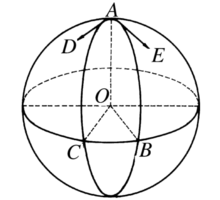
球面角球面角(spherical angle)是一种特殊的球面图形,指由球面上一点和以此点为公共端点的两条大圆弧所构成的球面图形,公共端点称为该球面角的顶点,两条大圆弧称为该球面角的边。若球面角的顶点是A,它的两条边分别通过点B,C(如图3),则该球面角可以记为∠BAC或∠CAB,球面角的度量有以下三种方法:
1.用由平面AOC和AOB所构成的二面角来度量。
2.用以球面角顶点为极的大圆,被该球面角截得的大圆弧BC之长来度量。
3.用过顶点的两条边的切线所夹的角(平面角)∠DAE来度量。
球面角也可以定义锐角、直角或钝角,小于π/2的球面角称为锐球面角,等于π/2的球面角称为直球面角,大于π/2的球面角称为钝球面角2。
解斜角球面三角形相关定理及公式以下规定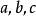 代表任意球面三角形的边,
代表任意球面三角形的边,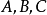 为相应的对角,
为相应的对角,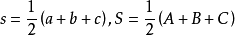 ,
,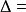 三角形的面积,E为三角形的球面角盈,
三角形的面积,E为三角形的球面角盈,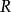 是三角形所在的球的半径,
是三角形所在的球的半径,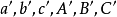 分别为配极三角形相应的元素3。
分别为配极三角形相应的元素3。
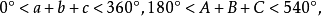
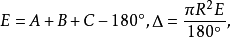
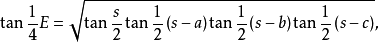
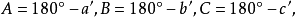
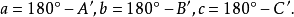 正弦定理:
正弦定理:
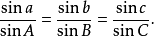 边的余弦定理:
边的余弦定理:
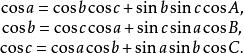 角的余弦定理:
角的余弦定理:
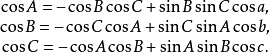 正切定理:
正切定理:
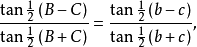
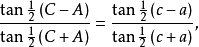 半角公式:
半角公式:
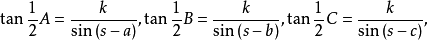 式中
式中
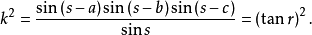 半边公式:
半边公式:
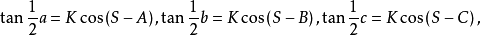 式中
式中
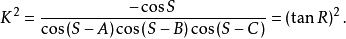 高斯公式:
高斯公式:
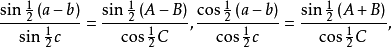
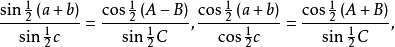 讷皮尔类比:
讷皮尔类比:
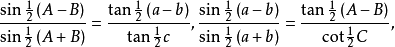
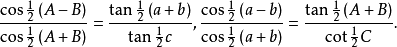 半正矢公式
半正矢公式
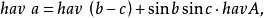
确定所求元素的象限的规则确定斜角球面三角形所求元素的象限的规则:
(a)若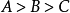 ,则
,则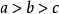 。
。
(b)其值距90°最远的一个边(角)与其对角(边)同在一个象限。
(c)任意两个边之和的一半与其对角之和的一半在相同的象限3。
斜角球面三角形解法小结
|| || 表1 斜角球面三角形解法
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国