[科普中国]-互反方程

概念

互反方程(reciprocal equation)是一种特殊的代数方程。数域P上的方程a0xn+a1xn-1+…+an=0 (a0≠0)的系数若满足an=a0，an-1=a1，…，则称此方程为互反方程。当n为奇数时，x=-1是它的根；当n为偶数2m时，解此方程相当于解一个m次方程与一个二次方程。数域P上的方程是互反方程当且仅当它的倒数方程与该方程同解，即α为方程的根当且仅当1/α也为其根。1

代数方程指多项式方程，其一般形式为：

是代数学中最基本的研究对象之一。

在20世纪以前，解方程一直是代数学的一个中心问题。二次方程的求解问题历史久远。在巴比伦泥板中(公元前18世纪)就载有二次方程的问题。古希腊人也解出了某些二次方程。中国古代数学家赵爽(公元3世纪)在求解一个有关面积的问题时，相当于给出二次方程的一个根。7世纪印度数学家婆罗摩笈多给出方程x2+px-q=0的一个根的公式：

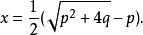一元二次方程的 一般解法是9世纪阿拉伯数学家花拉子米建立的。

对三次方程自古以来也有很多研究，在巴比伦泥板中，就有相当于三次方程的问题。阿基米德也曾讨论过方程x3+a=cx2的几何解法。11世纪波斯数学家奥马·海亚姆创立了用圆锥曲线解三次方程的几何方法，他的工作可以看作是代数与几何相结合的最早尝试。但是三次、四次方程的一般解法(即给出求根公式)，直到15世纪末也还没有被发现。意大利数学家帕乔利在1494年出版的著作中还说：“x3+mx=n，x3+n=mx(m，n为正数)现在之不可解，正像化圆为方问题一样。”但到16世纪上半叶，三次方程的一般解法就由意大利数学家费罗、塔尔塔利亚和卡尔达诺等得到，三次方程的求根公式最早出现在卡尔达诺的《大术》(1545)之中。四次方程的求根公式由卡尔达诺的学生费拉里首先得到，也记载于卡尔达诺的《大术》中。

在16世纪末到17世纪上半叶，数学家们还探讨如何判定方程的正根、负根和复根的个数。卡尔达诺曾指出一个实系数方程的复根是成对出现的，牛顿在他的《广义算术》中证明了这一事实。笛卡儿在他的《几何学》中给出了正负号法则(通称笛卡儿法则)，即多项式方程f(x)=0的正根的最多数目等于系数变号的次数，而负根的最多数目等于两个正号和两个负号连续出现的次数。但笛卡儿本人没有给出证明，这个法则是18世纪的几个数学家证明的。牛顿在《广义算术》中给出确定正负根数目上限的另一法则，并由此推出至少能有多少个复数根。

研究代数方程的根与系数之间的关系，也是这一时期代数学的重要课题。卡尔达诺发现方程所有根的和等于x的系数取负值，每两个根的乘积之和等于x的系数，等等。韦达和牛顿也都在他们的著作中分别叙述了方程的根与系数之间的关系，现在称这个结果为韦达定理。这些工作在18世纪发展为关于根的对称函数的研究。

另一个重要课题是今天所谓的因子定理。笛卡儿在他的《几何学》中指出，f(x)能为(x-a)整除，当且仅当a是f(x)=0的一个根。由此及其他结果，笛卡儿建立了求多项式方程有理根的现代方法。他通过简单的代换，把方程的首项系数化为1，并使所有系数都变为整数，这时他判断，原方程的各有理根必定是新方程常数项的整数因子。牛顿还发现了方程的根与其判别式之间的关系，他在《广义算术》中还给出了确定方程根的上界的一些定理。此外，数学归纳法也在18世纪末开始明确地用于代数学中。

18世纪以后，数学家们的注意力开始转向寻求五次以上方程的根式解。经过两个多世纪的努力，在欧拉、旺德蒙德、拉格朗日、鲁菲尼等人工作的基础上，在19世纪上半叶，阿贝尔和伽罗瓦几乎同时证明了五次以上的方程不能用公式求解。他们的工作开创了用群论的方法来研究代数方程的解的理论，为抽象代数学的建立开辟了道路(见置换群和伽罗瓦理论)。

代数方程理论的另一个问题是“一个方程能有多少个根”。中世纪阿拉伯和印度的数学家们都已认识到二次方程有两个根。到了16世纪，意大利数学家卡尔达诺引入了复数根，并认识到一个三次方程有3个根，一个四次方程有4个根，等等。荷兰数学家吉拉尔在1629年曾推测并断言：任意一个n次方程，如果把复根算在内并且k重根算作k个根的话，那么它就有n个根。这就是代数基本定理。这个定理在18世纪被许多著名的数学家认识到并试图证明之，直到1799年高斯才给出第一个实质性的证明。

对代数方程理论的研究，使数学家们引进了在近世代数中具有头等重要意义的新概念，这些新概念很快被发展成为有广泛应用的代数理论。2

倒数方程倒数方程亦称反商方程。一种特殊方程。即根的倒数亦为其根的整式一元方程。如果一元n次方程f(x)=0的根和f(1/x)=0的根完全相同，则称f(x)=0是一元n次倒数方程。它有下面两种形式：

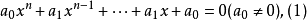
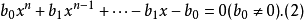
方程(1)称为第一类型倒数方程，亦称互反方程；方程(2)称为第二类型倒数方程。它的特点是首项系数和常数项，x的n-1次项系数和一次项系数，…，x的n-k次项系数和x的k次项系数，或是都相等，或是都相差一个负号。当n为偶数时，设n=2m，倒数方程可写为：

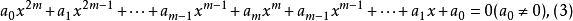
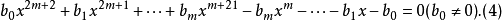
方程(3)称为第一类型偶次倒数方程，方程(4)称为第二类型偶次倒数方程。应该注意到方程(4)正中间的一项系数bm+1为零。当n为奇数时，设n=2m+1，倒数方程可写为：

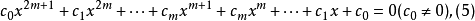
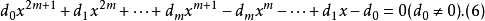
方程(5)称为第一类型奇次倒数方程，方程(6)称为第二类型奇次倒数方程。第二类偶次倒数方程(4)有根±1，求出根±1后可以化为一个形如方程(3)的2m次方程；第一类奇次倒数方程(5)有根-1，求出根-1后也可以化为一个形如方程(3)的2m次方程；第二类奇次倒数方程(6)有根1，求出根1后仍可以化为一个形如方程(3)的2m次方程。因此，方程(4)，(5)，(6)分别求出根±1，-1或1以后，所得的降次方程都是第一类偶次倒数方程，所以，第一类偶次倒数方程又称为标准型倒数方程。3