分类
旋轮类曲线可分为:外切外摆线、渐开线、内切外摆线、内摆线和直滚摆线。该分类的规律是:
(1)从外切外摆线到渐开线是滚圆曲率半径由小变无限大;
(2)从渐开线到内切外摆线是滚圆曲率改变方向
(3)从内切外摆线到内摆线是滚圆曲率半径由大变到小于基圆半径;
(4)从内摆线到直滚摆线是基圆曲率半径由小变无限大。
从这个变化规律可以看出摆线和渐开线是性质上相同的曲线,可以把它们归入一族,将它们取名为摆线族曲线。
外切外摆线外切外摆线是指:滚圆与基圆外切并沿基圆作纯滚动时,滚圆上定点的轨迹是外切外摆线。如图1所示。
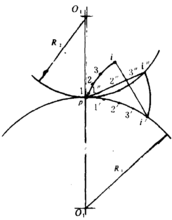
渐开线若滚圆曲率半径加大到无限大,圆周展成一条直线,该直线与基圆相切并沿基圆作纯滚动,直线上定点的轨迹为渐开线。如图2所示。
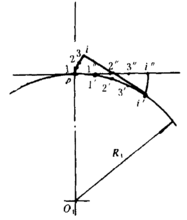
内切外摆线若上述沿基圆滚动的直线向下弯曲,变成一个比基圆半径更大的滚圆,该滚圆与基圆内切并沿基圆作纯滚动,滚圆上定点的轨迹是内切外摆线。如图3所示。
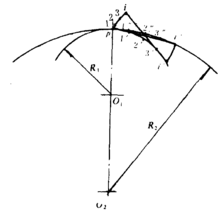
内摆线若内切外摆线滚圆的曲率半径缩小到小于基圆半径,该滚圆与基圆内切并沿基圆作纯滚动,滚圆上定点的轨迹为内摆线。如图4所示。
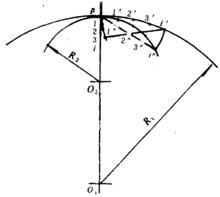
直滚摆线若内摆线的基圆半径加大到无限大,基圆圆周展成一条直线,滚圆与该直线相切并沿直线作纯滚动,滚圆上定点的轨迹为直滚摆线。如图5所示。
摆线族曲线的基本性质摆线族曲线有以下两种性质:
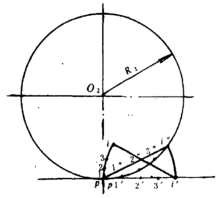
(1) 广义的滚圆(弧线或直线)与广义的基圆(弧线或直线)相切,它们在滚动过程中走过的行程相等(如图1所示)。根据这一性质就有:

(2) 广义滚圆(弧线或直线)上任意两点作正向和反向滚动所形成的轨迹具有完全的对称性(如图1所示)。根据这一性质就有1:
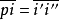
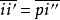




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国