[科普中国]-五次曲线

简介

在数学中，平面实数代数曲线是欧几里得平面上的坐标集合，其坐标是两个变量中的一些多项式的零点。 更一般来说，代数曲线是相似的，但是可以嵌入在较高维度空间中或者在一些更通用的场上被定义。

例如，单位圆是一个实数代数曲线，是多项式x² + y²=1的点的集合。

各种技术考虑导致多项式的复杂零被认为属于曲线。此外，代数曲线的概念已经被推广，以允许定义多项式的系数和曲线的点的坐标属于任何场，导致以下定义。

在代数几何中，在域k上定义的平面仿射代数曲线是K²的坐标集合，其坐标是具有k系数的一些双变量多项式的零点，其中K是k的一些代数闭合扩展。坐标为k的曲线的点是曲线的k点，并且是曲线的k部分。

例如，（2，√-3）是由x² + y² - 1 = 0定义的曲线点，通常的单位圆是该曲线的实部。术语“单位圆”可以指所有的复杂点，也可以指实际点，从上下文中通常清楚的确切含义。方程式x² + y² + 1 = 0定义了一个代数曲线，其实部为空。

更一般地，可以考虑不包含在平面中但在更高维度的空间中的代数曲线。不包含在某个平面中的曲线称为偏斜曲线。扭曲代数曲线的最简单的例子是扭曲的立方体。人们还可以考虑投影空间中包含的代数曲线，以及与在仿射或投影空间中嵌入的独立定义的代数曲线。这导致代数曲线的最一般定义：

在代数几何中，代数曲线是维度一的代数变量。2

在欧几里得几何中欧几里德平面中的代数曲线是其坐标是双变量多项式方程p（x，y）= 0的解的点集合。该方程通常称为曲线的隐式方程，通过与曲线相反的曲线是明确定义y作为x的函数的函数的图形。

使用这样一个隐式方程给出的曲线，第一个问题是确定曲线的形状并绘制曲线。这些问题并不像在功能图中的情况那样容易解决，对于这种函数，可以容易地为x的各种值计算y。定义方程是一个多项式的事实意味着曲线具有一些可能有助于解决这些问题的结构性质。

每个代数曲线可以被唯一地分解成有限数量的平滑单调弧（也称为分支），通过有时被称为“显着点”的某些点连接。平滑单调弧是在x轴的开放间隔上定义和单调的平滑函数的曲线图。在每个方向上，弧线是无界的（通常称为无限弧），或者具有一个终点，它是一个奇异点（这将在下面定义）或一个切线平行于一个坐标轴的点。

例如，对于图的Tschirnhausen立方，有两个无限弧，其原点（0,0）为终点。这一点是曲线的唯一奇点。有两个弧具有这个奇异点作为一个端点并且具有水平切线的第二终点。最后，还有另外两个弧，其中这些点具有水平切线作为第一个终点，并且将具有垂直切线的唯一点与第二个终点共享。另一方面，正弦曲线肯定不是代数曲线，具有无限数量的单调弧。

要绘制一个代数曲线，重要的是要知道它们的显着点和切线，无限分支及其渐近线（如果有的话）以及圆弧连接它们的方式。也可以将拐点考虑在内。当所有这些信息在纸张上绘制时，曲线的形状通常相当清楚。如果不是，可以添加其他几个点和它们的切线，以获得曲线的良好描述。3

非平面代数曲线代数曲线是维度一的代数变量。这意味着维数n的仿射空间中的仿射曲线由n个变量中的至少n-1个多项式定义。为了定义一个曲线，这些多项式必须产生Krull维1的主要理想。这种情况在实践中不容易测试。因此，可以以下列方式来表示非平面曲线。

让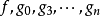是两个变量x1和x2中的n个多项式，使得f是不可约的。维度n的仿射空间中的点，其坐标满足方程和不等式：

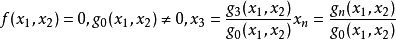
是有限数量的点被删除的代数曲线的所有点。该曲线由多项式h的理想的发生器系统定义，使得其存在整数kk使得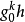属于由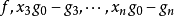。该表示是由f定义的曲线和平面曲线之间的有理等价。每个代数曲线都可以这样表示。然而，可能需要变量的线性变化，以使得几乎总是将投影注入到两个第一变量上。当需要改变变量时，几乎每一个变化都是方便的，一旦它被定义在一个无限的领域。

该表示允许我们从其平面投影的相应属性容易地推导出非平面代数曲线的任何属性，包括其图形表示。

对于由其隐式方程定义的曲线，曲线的上述表示可以从Gröbner基础中轻易地推导出块排序，使得较小变量的块为（x1，x2）。多项式f是基数中唯一依赖x1和x2的唯一多项式。通过选择i = 3，...，n，在xi中为线性的多项式，并且仅依赖于x1，x2和xi来获得分数gi / g0。如果这些选择是不可能的，这意味着方程式定义一个不是多样性的代数集合，或者该种类不是维度一，或者必须改变坐标。后一种情况发生在f存在且唯一的情况下，并且对于i = 3，...，n，存在多项式，其前导单项只取决于x1，x2和xi。4

代数函数域代数曲线的研究可以减少到不可约代数曲线的研究：不能写成两个较小曲线的并集的曲线。直到双等效，字段F上的不可约曲线分别等价于F上的一个变量中的代数函数字段。这样的代数函数字段是F的字段扩展K，其包含超过F的元素x， K是F（x）的有限代数扩展，它是不确定x在F上的理性函数的领域。

例如，考虑复数的字段C，我们可以在C中定义C中的有理函数的字段C（x）。如果y² = x³-x-1，则字段C（x，y）是椭圆函数领域。元素x不是唯一确定的;该场也可以被认为是例如C（y）的扩展。对应于函数域的代数曲线只是C2中满足y² = x³-x-1的点（x，y）集合。

如果字段F不是代数关闭的，那么函数字段的观点比考虑点的轨迹更加一般，因为我们包括例如没有点的“曲线”。例如，如果基字段F是实数的字段R，则x² + y² = -1定义了R（x）的代数扩展字段，但是被认为是R2的子集的相应曲线没有点。方程式x² + y² = -1在方案意义上（R中有限类型的积分，分离的一维方案）定义了R上的不可约代数曲线。在这个意义上，在F之间的不可约代数曲线（直到双等效）和一个变量中的代数函数域之间的一对一对应关系一般。

两条曲线可以是双等效的（即具有同构函数域），而不是同构的曲线。当处理非奇异曲线时，情况变得更加容易，即那些缺乏奇点的曲线。当且仅当它们的函数域是同构的时，场上的两个非奇异投影曲线是同构的。

特森定理是关于代数闭合场上的代数曲线的函数域。5

理性曲线一个合理的曲线，也称为单轨曲线，是任意一条曲线，它们与一条线相当，它们可能是一条投影线；因此，我们可以在一个不确定的F（x）中用理性函数的场来识别曲线的函数域。如果F代数闭合，这相当于零类曲线;然而，在真实代数变量x² + y² = -1上定义的所有实数代数函数的领域是不属于理性函数域的零属性的领域。

具体来说，通过以单个参数t定义的n个有理函数，可以将尺寸n超过F的合理曲线参数化（除了孤立的异常点）;通过清除分母，我们可以将其转化为投影空间中的n + 1个多项式函数。一个例子就是理性的正态曲线。

在F上定义的任何锥形截面是F的合理点，是一个合理的曲线。通过合理点绘制具有斜率t的线，并与平面二次曲线交点进行参数化;这给出了具有F-有理系数和一个F-有理根的多项式，因此另一个根也是F-合理（即属于F）。

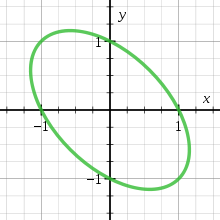例如，考虑椭圆x² + xy + y² = 1，其中（-1,0）是一个有理点。用（-1,0），y = t（x + 1）的斜率t绘制一条线，在椭圆方程中代入，求解x，得到：

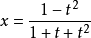
那么我们可以得到y的等式：

其定义了椭圆的合理参数化，因此显示椭圆是一个有理曲线。给出椭圆的所有点，除了（-1,1），对应于t =∞；因此，整个曲线由实际投影线参数化。

在投影空间中可以考虑这样一个合理的参数化，将第一个投影坐标与参数化的分子相等，最后一个投影坐标与公分母相等。由于参数在投影行中定义，所以参数中的多项式应该是均匀的。例如，上述椭圆的投影参数化是

在这些方程之间消除T和U，我们再次得到椭圆的投影方程：

这可以通过以上等式均匀化而直接获得6。