平面上一定点(-a,0),如果由这一点向y轴引射线交于P点,并在这射线上取两点M1、M2,使PM1=PM2=PO,则M1、M2点的轨迹就叫做环索线,它的普通方程是:y2(x-a)+x2(x+a)=0,(a>0)。
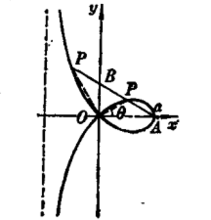
定义自定点任意引一直在此直线上截取一点P,使点P到此直线与Y轴的交点B的距离等于B到原点的距离。则点P的轨迹称为环索线(stropboid)1。
环索线的方程直角坐标方程设定点A的坐标为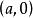 ,环索线的直角坐标方程为
,环索线的直角坐标方程为

极坐标方程环索线的参数方程为
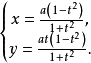 其中
其中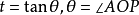 ,极坐标方程为
,极坐标方程为
 曲线的顶点为
曲线的顶点为 ,二重点
,二重点 ,渐近线
,渐近线 。圈套所围的面积
。圈套所围的面积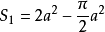 。曲线与渐近线之间的面积:
。曲线与渐近线之间的面积: 。
。
环索线有关名词简介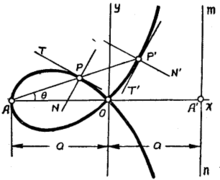
①极点 如A点;
如A点;
②结点 如
如 ;
;
③极轴 如
如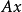 (亦为环索线的对称轴);
(亦为环索线的对称轴);
④动径 如
如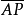 ;
;
⑤动径角 动径与极轴的夹角
动径与极轴的夹角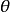 ;
;
⑥切线 同摆线定义,如
同摆线定义,如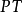 ;
;
⑦法线 如
如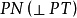 ;
;
⑧渐近线 距极点等于
距极点等于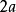 且垂直于极轴的直线,如mn1。
且垂直于极轴的直线,如mn1。
相关性质①环索线是关于极轴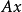 对称的图形;
对称的图形;
②环索线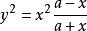 的渐近线
的渐近线 。
。
③过环索线上任一点 的切线与动径夹角(
的切线与动径夹角(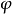 )的正切(
)的正切(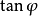 )等于
)等于 。
。
④过环索线上任意一点 的直线,与动径夹角(
的直线,与动径夹角(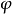 )的正切(
)的正切(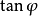 )若等于动径角(
)若等于动径角(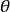 )的余弦(
)的余弦( ),则此直线是过该点
),则此直线是过该点 的切线1。
的切线1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国