[科普中国]-对偶范数

定义

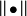令 为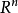 上的范数。对应的**对偶范数，**用 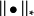表示，定义为

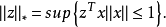
上式含义为: 对于某一个的范数小于1的向量 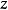， 与 的内积最大值就是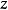 的对偶范数，对偶范数也可以解释为 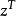的算子范数1。

对偶空间给定一个系数域为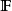 赋范向量空间（比如说一个巴拿赫空间）E（其中 通常是实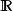数域 或复数域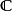 ），所有从E到 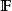上的连续线性映射（也称为连续线性泛函）的集合称为E的（连续）对偶空间，记作：E'。2

证明可以证明，E′是一个向量空间。其上可以装备不同的范数。对偶范数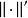（ ）是一种自然的范数定义方式，定义为：

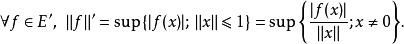
由于E′中的元素的是连续线性泛函，所以按照以上定义的范数必然存在，是一个有限正实数。引进了对偶范数后，E′成为一个赋范线性空间。可以证明，E′在对偶范数下必然是完备的，所以E′是巴拿赫空间。

性质对偶范数的对偶就是原范数：在有限维的向量空间中，对所有 有 .

向量范数

lp互lq互为对偶函数，需要满足条件：

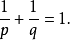
2. 矩阵范数

矩阵的谱范数的对偶范数为核范数。

例子给定两个大于1的实数p和q。如果两者满足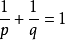： ，那么序列空间 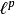和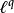 互相是对偶空间（在同构的意义上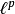）。 装备的是序列p-范数之时，它的对偶空间装备的对偶范数可以和装备了序列q-范数的 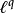建立等距同构。当p=q=2时，以上性质说明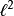， 和自身对偶。