[科普中国]-模2运算

模2运算是一种二进制算法，CRC校验技术中的核心部分。与四则运算相同，模2运算也包括模2加法、模2减法、模2乘法、模2除法四种二进制运算。与四则运算不同的是模2运算不考虑进位和借位，模2算术是编码理论中多项式运算的基础。模2算术在其他数字领域中的应用也是很广泛的。

模二运算移位寄存器的每一级只可能有两种不同的存数(或状态)，分别用0和1来表示。这里， 0和1不再具有一般数量的含义，而只具有逻辑含义。对于这样一种只包含0和1两个元素(符号)的集合(叫做二元集)来说，普通的四则运算不再适用，因而必须重新规定一种新的运算规则。所谓模2运算就是这样一种新的运算规则。1

模2运算是一种二进制算法，CRC校验技术中的核心部分。与四则运算相同，模2运算也包括模2加、模2减、模2乘、模2除四种二进制运算。而且，模2运算也使用与四则运算相同的运算符，即“+”表示模2加，“－”表示模2减，“×”或“·”表示模2乘，“÷”或“/”表示模2除。与四则运算不同的是模2运算不考虑进位和借位，即模2加法是不带进位的二进制加法运算，模2减法是不带借位的二进制减法运算。这样，两个二进制位相运算时，这两个位的值就能确定运算结果，不受前一次运算的影响，也不对下一次造成影响。

模二加法所谓“模2加法”就是0和1之间的加法，其中0+0 =0，1+0 =0+1 =1，1+1=0(!)。这种运算在通信和计算机上是常用的，而且并不神秘．你可以把0和1分别想成是“偶数”和“奇数”，那么前两个式子分别代表：偶数加偶数等于偶数，奇数加偶数等于奇数，而式1+1=0就是奇数加奇数等于偶数．对于任意多个数a1，a2，…，am（每个都是0或1），可以把它们做模2加法a1+a2+…+am。不难看出，当这m个数中有奇数个1时，结果为1，否则结果为0。

现在对二进制数定义模2加法，规则非常简单：即每个数位上分别作模2加法，由此得出一个新的二进制数，例如[ 1101]+[111]+[101]=[1111]，写成算式为

个位数字共有3个1，所以模2加为1（不进位）。同样的，其他数位上也均有奇数个1，不同数位之间彼此无关地运算，所以模2加法是不进位的加法。2

模二减法模2减法是一种不考虑借位的减法,其定义如下：

0-0=0

1-1=0

1-0=0

0-1=1

同样，第四式代表了模2减法的特征，从它也可得出2=0及+1=-1的结论。在多位模减法中，每位都按上述定义进行运算，不考虑借位问题。例如：

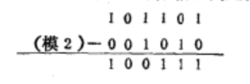
此结果和前面模2加法的结果完全一样，进而发现关于模2运算的一个重要特点，模2加法和模2减法实际上是一回事，所有用模2减法的地方都可用模2加法来代替，故不用给模2减法定义专用的符号。

模2加的定义可以得出一个重要结论：**奇数个1相加得1，偶数个1相加得0。**这个结论在奇偶校验中是很有用的。3

模二乘法一位数的模2乘法定义如下：

0×0=0

0×1=0

1×0=0

1×1=1

多位数的模2乘法与普通乘法一样演算,如：

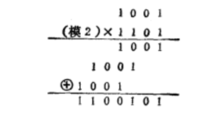
唯一的区别是，部分积相加时按模2加，即奇数个1相加得1，偶数个1相加得0。

模二除法模2除法是模2乘法的逆运算。如：

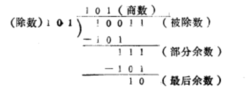
模2除法具有下列三个性质：

1、当最后余数的位数小于除数位数时，除法停止。

2、当被除数的位数小于除数位数时，则商数为0，被除数就是余数。

3、只要被除数或部分余数的位数与除数一样多，且最高位为1，不管其他位是什么数，皆可商1。

模2算术是编码理论中多项式运算的基础。模2算术在其他数字领域中的应用也是很广泛的。

本词条内容贡献者为:

李健 - 副教授 - 重庆邮电大学