[科普中国]-你知道量子计算机强在哪里吗？

导读：“一个量子比特可以同时处于0状态和1状态”，是什么意思？正确的理解是：经典比特是“开关”，只有开和关两个状态，而量子比特是“旋钮”，有无穷多个状态。为什么“n个量子比特包含2的n次方个比特的信息”？张真人，群众请你出来解释真武七截阵的原理！

—————————————————————————————

近年来，量子计算和量子通信（即“量子信息”）的成果层出不穷，吸引了公众越来越多的注意力。一个副产品是，借量子之名碰瓷的也如雨后春笋般活跃。前两天还有人问我所谓“量子能增程器”是不是真的，回答是：纯属子虚乌有！

心好累

碰瓷蹭热点之所以这么容易，是因为大多数人不明白量子科学的原理。虽然如此，像“量子能增程器”、“量子袜子”、“量子鞋垫”、“量子水”、“量子隐身衣”、“量子能量精华口服液”、“量子医学”这样的，还是比较容易分辨，因为一看就很不专业，压根没有这样的概念。（普朗克、爱因斯坦、海森堡、薛定谔、狄拉克等人怒问：我们费这么大劲搞出量子力学，居然只是给你们造袜子鞋垫的？）

我的内心是崩溃的

但下面这句话，用的就全是专业概念：“基于量子叠加原理，一个量子比特可以同时处于0状态和1状态。”

这是个超级常见的说法，你如果关心量子科技的新闻，我相信你肯定看到过类似的。但这个说法不能较真，一较真你会发现很难理解它实际说的是什么意思：是说量子比特同时处于两个状态？或者迅速在两个状态之间切换？或者处于一个不确定的状态？或者……时空分裂了？（脑洞开得太大，已阵亡）

量子比特迅速在两个状态之间切换？就像……佛山无影脚？！（动图）

在本文中，我会告诉读者，这句话实际讲的是什么意思，——用一种准确而且容易理解的方式。

还有一个更神的说法，看起来不仅专业而且定量，内容却似通非通，把我这个写过不少量子信息科普文章的人都搞糊涂了：

“一个电子可以存储一量子比特信息。如果需要2比特来描述1量子比特，那么需要4比特来描述2量子比特，需要16比特来描述4量子比特……”

说得明确一点就是，n个量子比特能存储2的n****次方个比特的信息。奇妙的是，说这番话的不是民科，而是2016年以来大火的《宝宝的物理学》系列的作者克里斯·费利（Chris Ferrie）博士。这是他在《宝宝的量子信息学》里写的。

《宝宝的量子信息学》

他甚至还做了一个幽默的比喻：为了存储我最喜欢的一个分子（咖啡因）的信息，就需要地球上所有的手机！

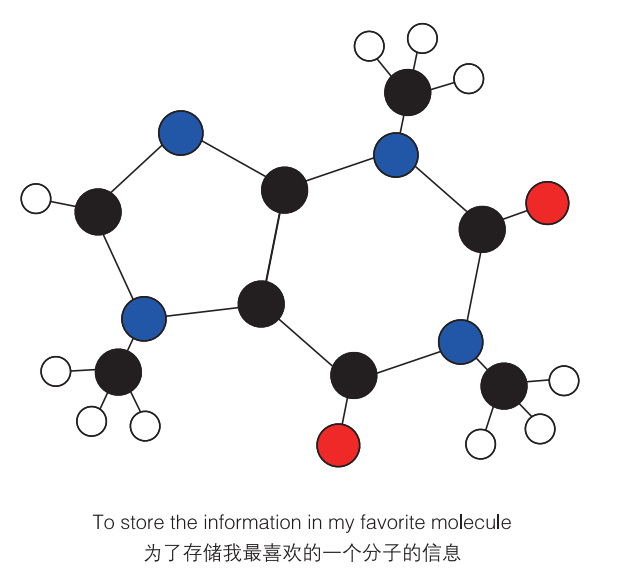
咖啡因分子

好好好，我们都知道你最喜欢喝咖啡了。在某种意义上，伟大的法国文学家巴尔扎克就是咖啡喝太多喝死的……

巴尔扎克

你可能在很多地方也看到过类似的说法。我严重怀疑这些作者看过金庸的《倚天屠龙记》，因为他们的描述就好像此书第十章《百岁寿宴摧肝肠》中武当派的“真武七截阵”：

“这七套武功分别行使，固是各有精妙之处，但若二人合力，则师兄弟相辅相成，攻守兼备，威力便即大增。若是三人同使，则比两人同使的威力又强一倍。四人相当于八位高手，五人相当于十六位高手，六人相当于三十二位，到得七人齐施，犹如六十四位当世一流高手同时出手。”

真武七截阵

这真是太好了……唯一的问题是，我知道这个说法实际表达的肯定不是字面上的意思，因为按照字面上，压根就不对。

这就很尴尬了

最近我咨询了一些量子信息的一线研究者，才明白了这个“真武七截阵”在什么意义上可以成立。当然，是类比的意义。在严格的意义上，它并不成立。

下面我们来从头解释起。

一、量子比特是什么？

“比特”是计算机科学的基本概念，指的是一个体系有且仅有两个可能的状态，一般用“0”和“1”来表示。典型的例子，如硬币的正、反两个面或者开关的开、关两个状态。

但在量子力学中，有一条基本原理叫做“叠加原理”：如果两个状态是一个体系允许出现的状态，那么它们的任意线性叠加也是这个体系允许出现的状态。

现在问题来了，什么叫做“状态的线性叠加”？为了说清楚这一点，最方便的办法是用一种数学符号表示量子力学中的状态，就是在一头竖直一头尖的括号“|>”中填一些表示状态特征的字符。这种符号是英国物理学家狄拉克发明的，称为“狄拉克符号”。

狄拉克的名著《量子力学原理》

在量子信息中，经常把两个基本状态写成|0>和|1>。而|0>和|1>的线性叠加，就是a|0> + b|1>，其中a和b是两个数，这样的状态称为“叠加态”。“线性”意味着用一个数乘以一个状态，“叠加”意味着两个状态相加，“线性叠加”就是把两个状态各自乘以一个数后再加起来。如果你学过线性代数，恭喜你，复习的机会来了~

叠加原理说的是：如果一个体系能够处于|0>和处于|1>，那么它也能处于|0>和|1>的任何一个叠加态。这样的一个体系，就是一个“量子比特”。

我们可以做一个比喻：经典比特是“开关”，只有开和关两个状态（0和1），而量子比特是“旋钮”，就像收音机上调频的旋钮那样，有无穷多个状态（所有的a|0> + b|1>）。

旋钮

现在，你明白“一个量子比特可以同时处于0状态和1状态”是什么意思了吧？它实际是说，量子比特可以处于|0>和|1>的叠加态。在一个时刻只会处于一个这样的确定的状态，既不是同时处于两个状态，也不是迅速在两个状态之间切换，也不是处于一个不确定的状态，更不是时空分裂。（黄飞鸿：可惜了我的佛山无影脚……）

不得不说，“同时处于0状态和1状态”是一个很容易令人糊涂的说法，好像禅宗的打机锋，远不如旋钮的比喻清楚易懂。更糟糕的是，读者可能会以为自己懂了，然后胡乱引申，造成更大的误解。在科普文章中，类似这样的令人似懂非懂的说法太多了，简直是遍地陷阱。

绊马索、陷马坑、连环陷阱！（动图，《秦时明月之万里长城》第15集《见龙在田》）

二、量子比特和经典比特的信息量怎么比？

了解了量子比特的概念后，你一方面会感到这是个巨大的扩展，一方面也会感到纳闷：从哪里能看出“n个量子比特包含2的n次方个比特的信息”？

张真人，群众请你出来解释真武七截阵的原理！

张三丰

实际上，稍微想想你就会发现，量子比特和经典比特的信息量根本不属于同一范畴，因为前者包含的是连续变量（任意的a、b两个数），而后者是离散变量（0或1）。你可以泛泛而言“量子比特包含的信息量比经典比特大得多”，但无法给出它们之间的定量关系，因为这就好像问：从0到1之间实数的个数，跟2相比是多少倍？回答是这个问题问得不好，因为从0到1之间的实数有无穷多个。

你是在逗我？

如果我们较真的话，甚至可以说：一个连续变量里就包含了无穷多的信息。因为我们可以把这个数写成一个二进制的无穷位小数（例如0.10011100101……），用小数点后第一位表示第一个比特的信息，第二位表示第二个比特的信息，如此等等。无论你有多少个比特的信息，一个小数里都塞得下。因此，整座图书馆的信息，甚至全世界所有的信息，都可以放在一个量子比特里！

你也许会感到有点不对。这种存储的思路，连量子比特都不用，只要传统的一个旋钮或者一把尺子就可以实现了，为什么我们没有这么做呢？

这是为什么呢？

原因在于，测量的精度是有限的。也许你可以准确地测出小数点后第一位，第二位也测得比较准，第三位就不太确定了，第四位就纯粹是蒙了，第五位以及更后面的，完全没有意义。因此，你貌似可以把任意多的信息存在一个连续变量里，但实际上取不出这么多信息。

幻觉，都是幻觉

三、真武七截阵的意思是……

那么，为什么许多人言之凿凿地说，n个量子比特包含2的n次方个比特的信息？

要让这句话有意义，关键在于：把a|0> + b|1>中的a和b这两个系数，当作两个比特的信息。这当然不是个严格的说法，因为把连续变量和离散变量混为一谈了。不过只要你姑且接受这种表述，你就可以明白，他们实际想说的是，“n个量子比特包含2的n****次方个系数”，这就是正确的了。

这是怎么算出来的？

对于一个量子比特，n = 1，体系可以取的状态是a|0> + b|1>，有a和b两个系数，系数的个数等于2的1次方。

对于两个量子比特，n = 2，体系可以取的状态是……是什么？

你也许会觉得，第一个量子比特的状态是a1|0> + b1|1>，第一个量子比特的状态是a2|0> + b2|1>，总共有4个系数。

错了！按照这种方式，当你有第三个量子比特时，只是增加a3|0> + b3|1>的两个系数，总共有6个系数。广而言之，每个量子比特提供两个系数，所以n个量子比特包含的系数个数就是2n，怎么会是2的n次方呢？

真正的关键在于，对于多量子比特的体系，基本的描述方式并不是“第一个量子比特处于某个态，第二个量子比特处于某个态……”，而是“系统整体处于某个态”。

系统整体可以处于什么态呢？再次回忆叠加原理（敲黑板）！是的，叠加原理对多粒子体系也适用。

敲黑板（动图，来自作者与观视频团队合作的视频节目“科技袁人”第二集《有人觉得中国科技太弱，因为全世界除了中国只有一个国家：“外国”》，https://www.bilibili.com/video/av17932364/）

所以，我们要做的就是找出多粒子体系可以处于的基本状态，而这些多粒子基本状态是由单粒子的|0>态和|1>态组合而成的。下面我们来看这些基本状态。

首先，你可以让每一个量子比特都处于自己的|0>态，这时系统整体的状态是所有这n个|0>态的直接乘积（称为“直积”），可以简写为|000…>，狄拉克符号里有n个“0”。

然后，在这个态的基础上，你可以让第一个量子比特变成自己的|1>态，这时系统整体的状态是|100…>，这也是一个直积态。

然后，在|000…>的基础上，你可以让另一个量子比特（比如说第二个）变成自己的|1>态，这时系统整体的状态是|010…>。这样，你可以走遍所有的由n-1个“0”和1个“1”组成的字符串。

然后，在|000…>的基础上，你可以让两个量子比特变成自己的|1>态。这样，你可以走遍所有的由n-2个“0”和2个“1”组成的字符串。

这个过程继续下去，最终你会把所有的量子比特都变成自己的|1>态，得到由n个“1”表示的|111…>这个态。在这个过程中，你得到了所有的由“0”和“1”组成的长度为n的字符串。

这样的态总共有多少个呢？第一位有2种选择，第二位也有2种选择，一直到第n位都是2种选择。所有这些选择乘起来，就是2的n次方种选择。注意是相乘，而不是相加。在高中学过排列组合、二项式定理的同学们，肯定都看明白了吧？

机智如我，早已看穿了一切

因此，n量子比特的系统有2的n次方个基本状态。它可以处于的一般状态，就是

这2的n次方个基本状态的线性叠加。可以写成c(000…) |000…> + c(100…) |100…> + c(010…) |010…> + … + c(111…) |111…>，其中每一个c都是一个系数，总共有2的n次方个这样的系数。

顺便说一下，这样的一个n粒子状态，有可能可以表示成n个单粒子状态的乘积，这时我们称它为“直积态”，但更常见的是不能表示成n个单粒子状态的乘积，这时我们称它为“纠缠态”。作为一个简单的例子，二粒子体系的(|00> + |11>) / √2就是一个纠缠态。你可以试着证明一下，很容易的~

一个慈祥的微笑

是的，上面讲的就是量子纠缠，就是那个你在很多文章里看到过、经常被宣传得神乎其神的东西。，其实它并不神秘，你如果想对量子纠缠获得更深入的了解，可以参见我的文章《你完全可以理解量子信息》的第7节“第三大奥义：纠缠”（https://mp.weixin.qq.com/s/LYVWlm6_tkCbmHrHxRI3cg）。

现在，我们终于明白“n个量子比特包含2的n次方个比特的信息”这句话实际的意思了。

张三丰：老道我也是蛮拼的！

真武七截阵没有动图，就给大家来一路太极拳吧（动图）

四、这个优势有多大用处？

用处很大，根本上，这就是量子计算机的优势所在。

具体而言，对于n个量子比特的量子计算机，一次操作就可以同时改变2的n次方个系数，相当于对n个比特的经典计算机进行2的n次方次操作。如果使用得当，这可以导致指数级的加速。这里的关键在于对量子纠缠的利用，如果没有纠缠态，只有直积态，那么你只有2n个系数，就没有加速可言了。

魔鬼藏在细节中，这里的魔鬼就是“如果使用得当”。为什么会有不得当的？因为把数据读出来是大问题。

在量子力学中，测量是一个独特的操作，跟非测量的过程服从不同的物理规律。不测量的时候，系统是做连续演化的，我们可以预测系统的状态。而在测量时，系统可能会发生突变，我们可能也会失去预测能力。

对量子力学中的测量的详细解释，可以参见我的文章《你完全可以理解量子信息》的第6节“第二大奥义：测量”（http://mp.weixin.qq.com/s/fkFEojysHLDn8uDUqcbxCA）。在这里，我们只要明白量子力学中测量的结果可能是不确定的，就足够了。

这意味着，虽然你一下子获得了2的n次方次操作的结果，但当你试图从中读出数据的时候，又会失去大部分信息。

坑爹啊！

由此导致的结果是，量子计算机的这个优势，需要非常巧妙的算法才能发挥出来。**只对少数特定的问题，人们才设计出了这样的算法。**而对于大多数的问题，量子计算机还没有表现出任何优势。

因此，当你再看到用真武七截阵来为量子计算机做宣传的文章时，就可以明白：他们说的只是潜力，不是一般情况。量子计算机不是普遍性地算得快，干什么都比经典计算机强，而是只对一些特定的问题比经典计算机算得快。

淡定，淡定

不过，这并不意味着量子计算机不堪大用。因为在目前已知的少数能发挥量子计算机优势的问题中，就包括两个非常重要的问题：因数分解和无结构数据库的搜索。对这两个问题的详细解释，可以参见我的文章《你完全可以理解量子信息》的第10节“量子因数分解和密码破解”（http://mp.weixin.qq.com/s/irNUF7bNxbRI0dn6rvxA1g）和第11节“量子搜索”（http://mp.weixin.qq.com/s/XXZ5qWugxeexOfvRV6-M3Q）。

因数分解的困难性是常用的密码体系RSA的基础，能快速分解因数就意味着能快速破解RSA。想想你的信用卡、支付宝，如果能被人快速破解，世界会变成什么样？（剁手党的噩梦.jpg）无结构搜索的应用就更广泛了，从交通流到制药，不计其数的问题都归结于搜索。即使找不到其他的问题，这两个也已经足够显示量子计算机的重要性了。

五、如果你问的就是存储……

最后，如果你的目标不是计算，而是单纯的存储，那么有一个定理会让你大跌眼镜：**从n个量子比特中能够读出的信息，最多就是n个经典比特！**这是苏联和俄罗斯物理学家亚历山大·豪尔沃（Alexander Holevo）在1973年证明的。在这个意义上，“n个量子比特包含2的n次方个比特的信息”的说法是完全错误的。

豪尔沃

也就是说，单就存储而言，量子比特没有任何优势。跟前面那个“一个连续变量存储整个世界的信息”的佯谬不同，这个结论甚至都不是由于测量的误差（即使你的测量完全精确都没用），而是由于量子力学的基本原理。

总结一下：量子比特的优势在于能处于两个基本状态的任何叠加态，但这个优势对于存储毫无价值，好处全都在计算上，而且只针对特定的能设计出巧妙算法的问题。虽然有这么多前提条件，但一旦能设计出这样的算法，让真武七截阵发动，就能发挥出神奇的威力！

现在，你对这个微妙的主题，理解深入多了吧？

至少，你用不着喝那么多咖啡了！每当让我在茶和咖啡中选择时，我总是毫不犹豫地选择茶~

同志哥，请喝一杯茶

作者简介：袁岚峰，中国科学技术大学化学博士，中国科学技术大学合肥微尺度物质科学国家实验室副研究员，科技与战略风云学会会长，微博@中科大胡不归，知乎@袁岚峰（https://www.zhihu.com/people/yuan-lan-feng-8）。

致谢：感谢中国科学院信息工程研究所杨理研究员在科学方面的指教。

请关注风云学会的微信公众平台“风云之声”，微信号fyvoice

知乎专栏：http://zhuanlan.zhihu.com/fengyun

一点资讯：http://www.yidianzixun.com/home?page=channel&id=m107089

今日头条：http://toutiao.com/m6256575842