现在复习一下导数的概念:如果差商极限
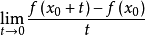 存在(有限),就把这极限值叫做
存在(有限),就把这极限值叫做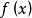 在
在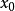 的导数(或微商),记作
的导数(或微商),记作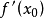 。单侧导数的定义:首先,设在
。单侧导数的定义:首先,设在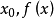 的右极限
的右极限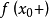 存在。如果以下差商右极限
存在。如果以下差商右极限
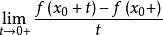 存在(有限),就把这极限值叫做
存在(有限),就把这极限值叫做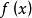 在
在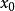 点的右导数;其次,设在
点的右导数;其次,设在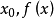 的左极限
的左极限 存在,如果
存在,如果
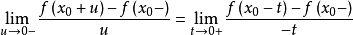 存在(有限),就把这极限值叫做
存在(有限),就把这极限值叫做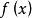 在
在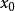 点的左导数。
点的左导数。
如果函数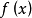 在闭区间
在闭区间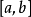 的每点有导数(在
的每点有导数(在 点只要右导数,在b点只要左导数),就说
点只要右导数,在b点只要左导数),就说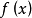 在区间
在区间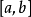 可微。其直观意义就是
可微。其直观意义就是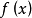 的图象在
的图象在 上处处有确定的切线。
上处处有确定的切线。
可以把在区间的可微推广为分段可微:如果能把闭区间 分成有限多个闭区间,使
分成有限多个闭区间,使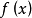 分别在每个小的闭区间上可微,就说函数
分别在每个小的闭区间上可微,就说函数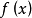 在
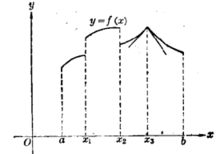
在 上分段可微。例如图1就表示一个在
上分段可微。例如图1就表示一个在 上分段可微的函数,分开的小闭区间就是
上分段可微的函数,分开的小闭区间就是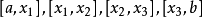 ,这样分开的小的闭区间叫做
,这样分开的小的闭区间叫做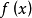 的可微区间。
的可微区间。
如果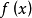 在整个数轴上有意义,且在数轴上的任何闭区间(长度有限)上分段可微,就说
在整个数轴上有意义,且在数轴上的任何闭区间(长度有限)上分段可微,就说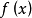 在整个数轴上分段可微。
在整个数轴上分段可微。
分段可微函数不但可能有有限跳跃,而且其图象可能有“尖点”,即左、右导数存在但不相等的连续点(如图1中 处)2。
处)2。
关于分段连续
(1)如果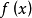 在数轴上分段连续,它在任何闭区间
在数轴上分段连续,它在任何闭区间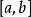 上分段连续,就是说,可把
上分段连续,就是说,可把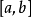 分成有限多个小的闭区间,
分成有限多个小的闭区间,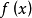 分别在这些小的闭区间上连续。这样,
分别在这些小的闭区间上连续。这样,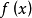 就分别在这些连续区间上可积,从而
就分别在这些连续区间上可积,从而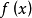 在
在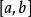 可积。
可积。
(2)如果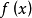 在数轴上分段连续,那么,在它的连续区间内部的点上,
在数轴上分段连续,那么,在它的连续区间内部的点上,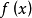 的极限存在,即左、右极限都存在且相等。在连续区间的右端点,例如在图1中区间
的极限存在,即左、右极限都存在且相等。在连续区间的右端点,例如在图1中区间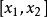 的右端点
的右端点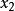 ,
,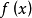 的左极限
的左极限 存在。但
存在。但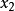 同时是右方相邻的连续区间
同时是右方相邻的连续区间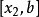 的左端点,故在
的左端点,故在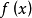 的右极限
的右极限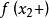 也存在。总而言之,在数轴上的任何点
也存在。总而言之,在数轴上的任何点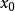 ,分段连续函数
,分段连续函数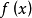 的左、右极限
的左、右极限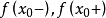 都存在。
都存在。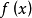 在
在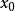 唯一可能的间断性是
唯一可能的间断性是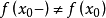 ,这种间断性称为有限跳跃。分段连续函数不能具有象
,这种间断性称为有限跳跃。分段连续函数不能具有象 在
在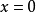 那样的间断性。
那样的间断性。
分段可微函数
(3)如果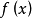 在数轴上分段可微,则它在可微区间上必连续,于是
在数轴上分段可微,则它在可微区间上必连续,于是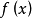 在数轴上分段连续,根据(1),知
在数轴上分段连续,根据(1),知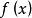 在任何闭区间上可积。
在任何闭区间上可积。
(4)通过类似(2)中的讨论可知,如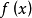 在数轴上分段可微,则在数轴上的任何点
在数轴上分段可微,则在数轴上的任何点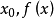 都具有左导数
都具有左导数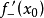 和右导数
和右导数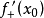 。
。
(5)设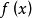 只是在长为T的区间
只是在长为T的区间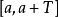 上给出的分段可微函数,把
上给出的分段可微函数,把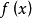 按周期T延拓到整个数轴上(仍用
按周期T延拓到整个数轴上(仍用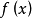 表示延拓后的函数)。那么,延拓后的
表示延拓后的函数)。那么,延拓后的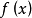 必是数轴上分段可微的函数。这时
必是数轴上分段可微的函数。这时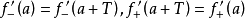 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国