[科普中国]-分位数回归模型

简介

分位数回归（英语：Quantile regression）是回归分析的方法之一。最早由Roger Koenker和Gilbert Bassett于1978年提出。

一般地，传统的回归分析研究自变量与因变量的条件期望之间的关系，相应得到的回归模型可由自变量的估计因变量的条件期望；分位数回归研究自变量与因变量的条件分位数之间的关系，相应得到的回归模型可由自变量估计因变量的条件分位数。相较于传统回归分析仅能得到因变量的中央趋势，分量回归可以进一步推论因变量的条件概率分布。分量回归属于非参数统计方法之一。1

回归分析回归分析（英语：Regression Analysis）是一种统计学上分析数据的方法，目的在于了解两个或多个变数间是否相关、相关方向与强度，并建立数学模型以便观察特定变数来预测研究者感兴趣的变数。更具体的来说，回归分析可以帮助人们了解在只有一个自变量变化时因变量的变化量。一般来说，通过回归分析我们可以由给出的自变量估计因变量的条件期望。

回归分析是建立因变数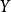（或称依变数，反应变数）与自变数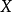（或称独变数，解释变数）之间关系的模型。简单线性回归使用一个自变量，复回归使用超过一个自变量（）。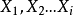

起源回归的最早形式是最小二乘法，由1805年的勒让德(Legendre)，和1809年的高斯(Gauss)出版。勒让德和高斯都将该方法应用于从天文观测中确定关于太阳的物体的轨道（主要是彗星，但后来是新发现的小行星）的问题。 高斯在1821年发表了最小二乘理论的进一步发展，包括高斯－马尔可夫定理的一个版本。

“回归”（或作“回归”）一词最早由法兰西斯·高尔顿（Francis Galton）所使用。他曾对亲子间的身高做研究，发现父母的身高虽然会遗传给子女，但子女的身高却有逐渐“回归到中等（即人的平均值）”的现象。

在1950年代和60年代，经济学家使用机械电子桌面计算器来计算回归。在1970年之前，它有时需要长达24小时从一个回归接收结果。

回归分析原理目的在于找出一条最能够代表所有观测资料的函数（回归估计式）。

用此函数代表因变数和自变数之间的关系。

回归模型回归模型主要包括以下变量：

未知参数，记为β，可以代表一个标量或一个向量。

自变量，X。

因变量，Y。

回归模型将Y和一个关于X和β的函数关联起来：。2

参阅曲线拟合

估计理论

广义线性模型

多元正态分布

皮尔逊积矩相关系数

信号处理

相关分析

多变量统计