在自然科学领域中,皮尔逊相关系数广泛用于度量两个变量之间的相关程度,其值介于-1与1之间。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的。这个相关系数也称作“皮尔逊积矩相关系数”。

图1中,几组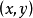 的点集,以及各个点集中
的点集,以及各个点集中 和
和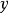 之间的相关系数。我们可以发现相关系数反映的是变量之间的线性关系和相关性的方向(第一排),而不是相关性的斜率(中间),也不是各种非线性关系(第三排)。请注意:中间的图中斜率为0,但相关系数是没有意义的,因为此时变量
之间的相关系数。我们可以发现相关系数反映的是变量之间的线性关系和相关性的方向(第一排),而不是相关性的斜率(中间),也不是各种非线性关系(第三排)。请注意:中间的图中斜率为0,但相关系数是没有意义的,因为此时变量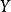 是0。
是0。
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:
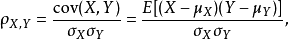
上式定义了总体相关系数,常用希腊小写字母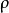 作为代表符号。估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母
作为代表符号。估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母  代表:
代表:
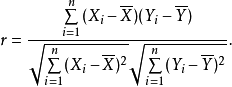
 亦可由
亦可由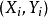 样本点的标准分数均值估计,得到与上式等价的表达式:
样本点的标准分数均值估计,得到与上式等价的表达式:
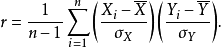 其中
其中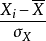 、
、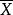 及
及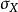 分别是对
分别是对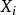 样本的标准分数、样本平均值和样本标准差。
样本的标准分数、样本平均值和样本标准差。
总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上(计算样本皮尔逊系数的情况),或者双变量分布完全在直线上(计算总体皮尔逊系数的情况),则相关系数等于1或-1。皮尔逊系数是对称的: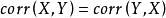 。
。
皮尔逊相关系数有一个重要的数学特性是,因两个变量的位置和尺度的变化并不会引起该系数的改变,即它该变化的不变量(由符号确定)。也就是说,我们如果把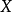 移动到
移动到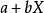 和把Y移动到
和把Y移动到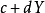 ,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)。我们发现更一般的线性变换则会改变相关系数:
,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)。我们发现更一般的线性变换则会改变相关系数:
由于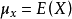 ,
,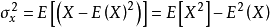 ,
,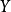 也类似, 并且
也类似, 并且
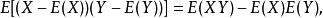 故相关系数也可以表示成
故相关系数也可以表示成
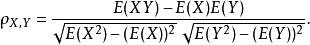
对于样本皮尔逊相关系数:
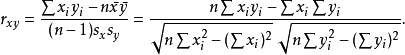
以上方程给出了计算样本皮尔逊相关系数简单的单流程算法,但是其依赖于涉及到的数据,有时它可能是数值不稳定的。
解释皮尔逊相关系数的变化范围为-1到1。 系数的值为1意味着X和Y可以很好的由直线方程来描述,所有的数据点都很好的落在一条直线上,且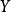 随着
随着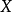 的增加而增加。系数的值为−1意味着所有的数据点都落在直线上,且
的增加而增加。系数的值为−1意味着所有的数据点都落在直线上,且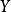 随着
随着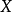 的增加而减少。系数的值为0意味着两个变量之间没有线性关系。
的增加而减少。系数的值为0意味着两个变量之间没有线性关系。
更一般的, 我们发现,当且仅当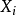 和
和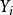 均落在他们各自的均值的同一侧, 则
均落在他们各自的均值的同一侧, 则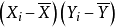 的值为正。 也就是说,如果
的值为正。 也就是说,如果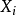 和
和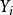 同时趋向于大于,或同时趋向于小于他们各自的均值,则相关系数为正。 如果
同时趋向于大于,或同时趋向于小于他们各自的均值,则相关系数为正。 如果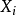 和
和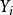 趋向于落在他们均值的相反一侧,则相关系数为负。
趋向于落在他们均值的相反一侧,则相关系数为负。
对于没有中心化的数据, 相关系数与两条可能的回归线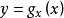 和
和 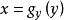 夹角的余弦值一致。
夹角的余弦值一致。
对于中心化过的数据 (也就是说, 数据移动一个样本平均值以使其均值为0), 相关系数也可以被视作由两个随机变量向量夹角  的余弦值。
的余弦值。
一些人倾向于是用非中心化的相关系数, 比较如下:
例如,有5个国家的国民生产总值分别为 10, 20, 30, 50 和 80 亿美元。 假设这5个国家 (顺序相同) 的贫困百分比分别为 11%, 12%, 13%, 15%, and 18% 。 令x和y分别为包含上述5个数据的向量:x= (1, 2, 3, 5, 8) 和y= (0.11, 0.12, 0.13, 0.15, 0.18)。
利用通常的方法计算两个向量之间的夹角 ,未中心化的相关系数是:
,未中心化的相关系数是:
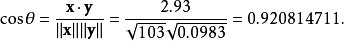 我们发现以上的数据特意选定为完全相关:
我们发现以上的数据特意选定为完全相关: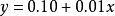 。 于是,皮尔逊相关系数应该等于1。将数据中心化 (通过
。 于是,皮尔逊相关系数应该等于1。将数据中心化 (通过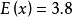 移动
移动 和通过
和通过 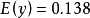 移动
移动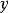 ) 得到
) 得到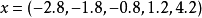 和
和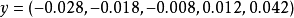 从中,
从中,
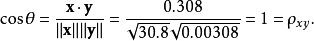
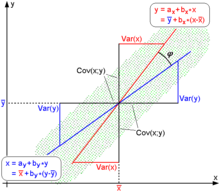
说明:图2中,回归直线: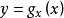 [红色] 和
[红色] 和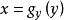 [蓝色]
[蓝色]
皮尔逊距离度量的是两个变量X和Y,它可以根据皮尔逊系数定义成 我们可以发现,皮尔逊系数落在
我们可以发现,皮尔逊系数落在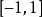 ,而皮尔逊距离落在
,而皮尔逊距离落在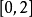 。
。
样本相关系数的平方, 亦称作coefficient of determination, 利用简单线性回归估计由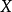 引起的
引起的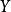 的变化。 一开始,
的变化。 一开始,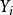 围绕它们平均值上的变化可以分解成
围绕它们平均值上的变化可以分解成
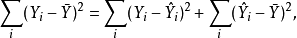
其中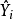 是作回归分析时的适应值。 整理后得
是作回归分析时的适应值。 整理后得
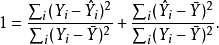
两个被加数是由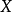 (右边)引起的
(右边)引起的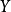 的变化和不是由
的变化和不是由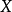 (左边) 引起的变化。
(左边) 引起的变化。
接下来, 我们利用最小方差回归模型, 使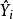 和
和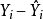 的样本协方差为0。 于是,观测数据和适应值的样本相关系数可以被写成1
的样本协方差为0。 于是,观测数据和适应值的样本相关系数可以被写成1
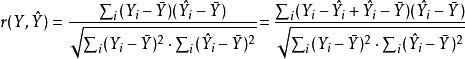

于是
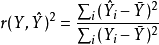 是由
是由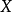 的线性方程引起的
的线性方程引起的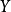 的平均变化。
的平均变化。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国