如果一个锥体的底面为圆形,顶点位于过底面中心的底面的垂线上,则这个锥体称为直圆锥(right circular cone)。直角三角形以其一直角边为轴旋转而成的旋转体是直圆锥。也可以说在初等几何中,一个锥体若底面为圆,而圆心恰为其顶点在底面上的射影,则称其为直圆锥。通常说圆锥多是指直圆锥1。
基本介绍以直角三角形的一条直角边所在的直线为轴,其余两边绕轴旋转360°所得到的几何体,叫做直圆锥,简称圆锥,如图1。
直角三角形旋转时,有一条直角边位于旋转轴上,另一条直角边旋转产生的圆面叫做圆锥的底面。斜边旋转时的每一个位置,叫做直圆锥的母线,旋转时产生的曲面叫做直圆锥的侧面。斜边位于轴上的端点叫做直圆锥的顶点。直圆锥的顶点和底面的距离(即顶点和底面圆圆心的距离)叫做直圆锥的高。
直圆锥的底面是圆。
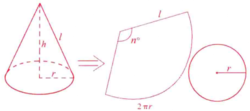
直圆锥的侧面沿母线剪开后在平面上展开,是一个扇形。它的半径等于直角三角形的斜边长,它的弧长等于直圆锥的底面圆的周长。图2就是直圆锥的侧面展开图2。

直圆锥的性质直圆锥的主要性质:
(1) 直圆锥的底面是个圆。它所在的平面垂直于圆的轴。
(2) 直圆锥的轴经过顶点和底面的圆心,底面圆心和顶点的连线是圆锥的高。
(3) 直圆锥的一切母线都交圆锥的顶点,并且都相等,各条母线与轴的夹角都相等。
(4) 用一个过直圆锥的顶点,并且和底面相交的平面去截直圆锥,所得的截面是一个等腰三角形。
(5) 垂直于轴的直圆锥截面是个圆。
圆锥体的体积与侧面积直圆锥体的体积等于它的底面积与高的积的三分之一。
若设圆锥体的体积为V,底面积为S,高为h,那么,圆锥体的体积公式为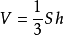 或
或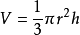 。
。
直圆锥体的侧面积等于它的底面的周长与母线长乘积的一半。
若圆锥的母线为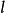 ,底面半径为
,底面半径为 ,侧面积为S,那么,圆锥体的侧面积公式为
,侧面积为S,那么,圆锥体的侧面积公式为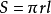 。
。
直圆锥的方程式由方程
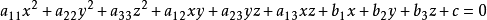 给出的曲面,叫做二次曲面。
给出的曲面,叫做二次曲面。
这个方程给出的可以不是曲面,而是具有更小维度的图形:直线,点或者甚至是空集合。这样的图形我们不列入二次曲面。
二次曲面称为圆锥,如果在某个直角坐标系中它用方程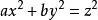 给出,其中
给出,其中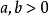 。在
。在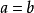 这种情况,圆锥称为旋转圆锥或者直圆锥。点
这种情况,圆锥称为旋转圆锥或者直圆锥。点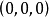 称为圆锥的顶点,而轴
称为圆锥的顶点,而轴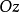 叫做圆锥的轴。
叫做圆锥的轴。
相关结论**【例1】**证明:顶点在坐标原点的直圆锥的方程形式为3
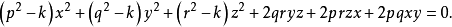
**证明提示:**设圆锥轴的方向用向量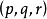 给出,向量
给出,向量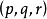 和
和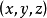 之间的角的余弦等于
之间的角的余弦等于
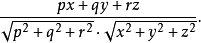 点
点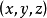 的集合,对于它这个余弦精确到符号相同,给出方程的形式为
的集合,对于它这个余弦精确到符号相同,给出方程的形式为
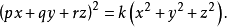
**【例2】**证明:如果圆锥
 是直圆锥,并且数
是直圆锥,并且数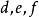 中一个等于零,那么这些数中还有一个等于零。
中一个等于零,那么这些数中还有一个等于零。
**证明提示:**根据上一问题数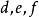 具有形式
具有形式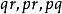 。如果这些数中有一个等于零,那么由数
。如果这些数中有一个等于零,那么由数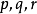 中一个等于零,则由数
中一个等于零,则由数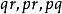 中还有一个等于零。
中还有一个等于零。
**【例3】**证明:圆锥
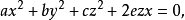 其中
其中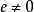 ,是直圆锥,当且仅当
,是直圆锥,当且仅当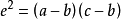 。
。
证明提示: 首先假设,圆锥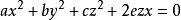 是直圆锥,根据问题①有
是直圆锥,根据问题①有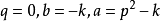 和
和 ,所以
,所以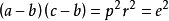 。
。
现在假设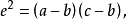 设
设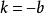 ,根据条件
,根据条件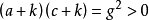 ,所以
,所以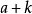 和
和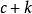 要么两个都正,要么两个都负,在必要时改变圆锥方程的所有系数的符号,可以认为,数
要么两个都正,要么两个都负,在必要时改变圆锥方程的所有系数的符号,可以认为,数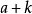 和
和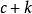 是正的,假设
是正的,假设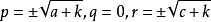 ,根据条件
,根据条件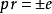 ,符号可以选择,使得成立等式
,符号可以选择,使得成立等式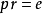 ,这时圆锥的方程化归为正如在问题①指出的这样的形式。
,这时圆锥的方程化归为正如在问题①指出的这样的形式。
【例4】直圆锥用不平行于它的轴的平面的截形,射影在垂直于圆锥的轴的平面上,证明:圆锥的轴相交射影于焦点。
**证明提示:**可以认为,圆锥的顶点位置在坐标原点,而它的轴沿着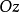 轴的方向,则圆锥的方程具有形式
轴的方向,则圆锥的方程具有形式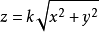 。坐标平面
。坐标平面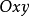 旋转后可以认为,截割平面的方程具有形式
旋转后可以认为,截割平面的方程具有形式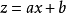 ,这样一来,圆锥截形在坐标平面
,这样一来,圆锥截形在坐标平面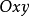 上的射影由方程
上的射影由方程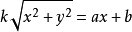 给出,这个方程可以改写为
给出,这个方程可以改写为
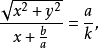 最后一个方程给出焦点在坐标原点,准线为
最后一个方程给出焦点在坐标原点,准线为 和离心率为
和离心率为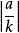 (由点到焦点的距离对点到准线距离的比等于离心率)的二次曲线3。
(由点到焦点的距离对点到准线距离的比等于离心率)的二次曲线3。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国