[科普中国]-预解方程

预解方程，又称预解式，港台地区译作豫解式，即我们常说的公式法解方程中的求根公式。普通一元二次方程的预解方程，在9世纪时就已经发现。目前初中二年级课本中有相关描述。

定义设 T 是作用在巴拿赫空间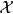 上的有界线性算子1，当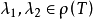时，预解方程为

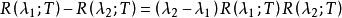
预解式一元二次方程普通一元二次方程的预解方程，在9世纪时就已经发现。在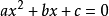中，。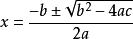

目前初中二年级课本中有相关描述。

一元三次方程16世纪，普通一元三次方程及一元四次方程的预解方程都被发现。

该预解方程推倒的主旨思想是通过换元将n次方程向(n-1)次方程转变，再用解(n-1)次方程的预解方程推出该方程预解式。

1505年，三次方程式预解方程已被Scipio Ferreo求出，之后冯塔纳也求出预解方程，并以严守秘密为条件传授给了卡尔丹，但卡尔丹不守信约，于1545年发表，后人称之为卡尔丹公式。之后Hudde于1650年发表了另一种解法。2

四次方程式预解式由费拉里于1540年前后推出。

一元四次以上方程1770年，拉格朗日将前人方法总结，并间接使用置换群的概念(尚未提出)，将各种解法归纳于一种原理下， 并证明普通五次方程没有预解方程，自此，近世代数拉开序幕。

1815年，柯西对置换进行了系统的研究，成为了置换群理论研究的先驱。

此后，阿贝尔、伽罗瓦两位天才数学家证明了n(n>4)次方程式没有有理与无理预解方程，并提出群论、域论这两个重要的数学概念，为日后的代数学研究奠下重要的基石。但这两个数学家都英年早逝，伽罗瓦20岁时因决斗逝去，阿贝尔27岁染重疾逝去，他们死后约半个世纪，他们的学说才被认同。2

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学