在数学上,线性化是找到线性近似的函数在给定的点。在研究的动力系统,线性化是评估局部的方法稳定性的的平衡点一的系统的非线性 微分方程或者离散的动力系统。这种方法用于工程,物理,经济和生态等领域。
线性化简介就是在一定的条件下作某种近似,或者缩小一些工作范围,而将非线性微分方程近似地作为线性微分方程来处理。用数学方法处理就是将变量的非线性函数展开成泰勒级数,分解成这些变量在某工作状态附近的小增量的表达式,然后略去高于一次小增量的项,就可以获得近似的线性函数。一个线性方程在实际应用中可以写作:
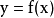
其中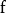 具有如下特性:
具有如下特性:
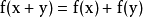
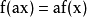
这里a不是向量
如果一个函数满足这样的特性就叫做线性函数。
因为线性的独特属性,在同类方程中对线性函数的解决有叠加作用。这使得线性方程最容易解决和推演。
线性方程在应用数学中有重要规律。使用它们建立模型很容易,而且在某些情况下可以假设变量的变动非常小,因此实际应用中把许多非线性方程 转化为线性方程来处理。
应用线性化方法是自然科学研究中的普遍方法。该方法是把高级次热力学、动力学方程,经过线性化操作(如取对数、取倒数、微扰)降为线性方程处理。1
函数的线性化 函数的线性化就是可以用于计算的线。线性化是近似函数输出的有效方法
函数的线性化就是可以用于计算的线。线性化是近似函数输出的有效方法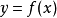 在任何
在任何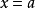 基于函数的值和斜率, 鉴于
基于函数的值和斜率, 鉴于 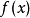 是可区分的
是可区分的 (要么
(要么 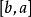 }) 然后
}) 然后 接近
接近 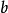 。简而言之,线性化近似于一个函数的输出
。简而言之,线性化近似于一个函数的输出 。
。
例如, 。但是,这将是一个很好的近似值
。但是,这将是一个很好的近似值 。
。
对于任何给定的功能 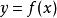 ,
, 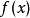 可以近似,如果它接近已知的可微点。最基本的要求是
可以近似,如果它接近已知的可微点。最基本的要求是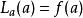 ,在哪里
,在哪里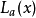 是线性化的
是线性化的 在
在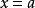 。给定一个点,方程的点斜率形式表示一条线的方程
。给定一个点,方程的点斜率形式表示一条线的方程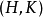 和斜坡
和斜坡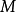 。这个方程的一般形式是:
。这个方程的一般形式是: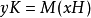 。
。
使用点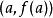 ,
, 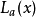 变
变 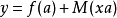 。因为微函数是局部线性,最好的斜率来代替在将是线的斜率切线到
。因为微函数是局部线性,最好的斜率来代替在将是线的斜率切线到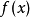 在
在 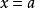 。
。
虽然当地线性的概念适用最给点任意接近至 那些比较接近的线性近似的工作相对较好。斜坡
那些比较接近的线性近似的工作相对较好。斜坡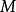 应该是,最准确地说,在那里的切线的斜率
应该是,最准确地说,在那里的切线的斜率 。
。
在视觉上,附图显示的是切线  在
在  。在
。在 ,在哪里
,在哪里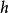 是任何小的积极或消极的价值,
是任何小的积极或消极的价值, 非常接近该点切线的值
非常接近该点切线的值  。
。
最后一个函数线性化的方程 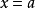 是:
是:

对于 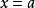 ,
, 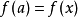 。该衍生物的
。该衍生物的 是
是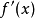 ,和斜坡
,和斜坡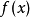 在
在  是
是 。
。
示例找到 ,我们可以使用这个事实
,我们可以使用这个事实 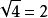 。线性化
。线性化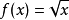 在
在 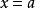 是
是 ,因为功能
,因为功能 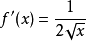 定义函数的斜率
定义函数的斜率  在
在 代入
代入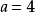 ,在4的线性化是
,在4的线性化是 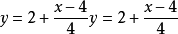 。在这种情况下
。在这种情况下 ,所以
,所以 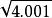 是近似的 .
是近似的 .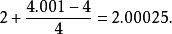 。真实值接近于2.00024998,所以线性化近似的相对误差小于百万分之一。
。真实值接近于2.00024998,所以线性化近似的相对误差小于百万分之一。
多变量函数的线性化函数线性化的等式 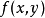 在一个点
在一个点 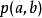 是:
是:

多变量函数线性化的一般方程 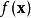 在一个点
在一个点 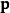 是:
是:
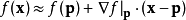
哪里 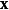 是变量的向量,
是变量的向量, 是线性化的兴趣点2。
是线性化的兴趣点2。
线性化的使用线性化使得使用工具来研究线性系统来分析给定点附近的非线性函数的行为成为可能。一个函数的线性化是它在感兴趣点附近泰勒展开的一阶项。对于由等式定义的系统

线性化系统可写成

 是感兴趣,
是感兴趣,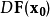 是雅可比的
是雅可比的 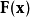 在
在 的评估。
的评估。
稳定性分析在自治系统的稳定性分析中,可以使用在双曲平衡点评估的雅可比矩阵的特征值来确定该平衡的性质。这是线性化定理的内容。对于时变系统,线性化需要额外的理由。
微观经济学在微观经济学中,决策规则可以在线性化的状态空间方法下近似。在这种方法中,欧拉方程的的效用最大化的围绕静止稳态线性化。然后找到一个独特的解决方案的结果系统的动态方程。
优化在数学优化中,成本函数和内部的非线性分量可以线性化,以便应用诸如Simplex算法的线性求解方法。优化的结果可以更有效地得到,并且是全局最优的确定性的3。
多物理学在多物理场系统中,涉及多个彼此相互作用的物理场的系统 - 可以执行关于每个物理场的线性化。该系统关于每个场的线性化导致线性化的单片方程系统,其可以使用单片迭代解决方案如牛顿 - 拉夫逊(Newton-Raphson)方法来求解。这样的例子包括导致电磁,机械和声场系统的MRI扫描仪系统4。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国