[科普中国]-累积分布函数

累积分布函数(Cumulative Distribution Function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。一般以大写CDF标记,，与概率密度函数probability density function（小写pdf）相对。

定义对于所有实数 ，累积分布函数定义如下：

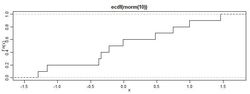
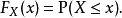即累积分布函数表示：对离散变量而言，所有小于等于a的值出现概率的和1。

性质1.有界性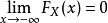

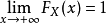
2.单调性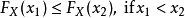

3.右连续性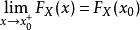 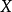之值落在一区间(a,b]之内的机率为

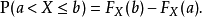一随机变数X的CDF与其pdf的关系为

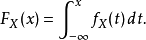
反函数若累积分布函数F是连续的严格增函数，则存在其反函数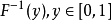。累积分布函数的反函数可以用来生成服从该随机分布的随机变量2。

设若是概率分布X的累积分布函数，并存在反函数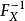。若a是[0,1)区间上均匀分布的随机变量，则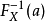服从X分布。

互补累积分布函数互补累积分布函数（complementary cumulative distribution function、CCDF），是对连续函数，所有大于a的值，其出现概率的和。

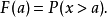
本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学