迷向直线(isotropic line)亦称极小直线,是射影几何的基本概念之一。指通过虚圆点的任意虚直线,迷向直线与无穷远直线的交点一定是虚圆点。迷向直线构成以点(1,i,0)或(1,-i,0)为中心的平行直线束,其斜率分别为i或-i,通过平面内任一有穷点有两条迷向直线,分别属于这两个直线束。迷向直线具有下列性质:1.虚直线是迷向直线的充分必要条件是它上面任意两个不同的有穷点的距离是零;2.一条迷向直线与另一条直线的交角是不定的1。
基本介绍定义定理1 平面内任何一圆通过无穷远直线上两个固定的共轭虚点。
定理2 通过两点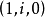 和
和 的常态二次曲线一定是圆(定理1的逆定理)。
的常态二次曲线一定是圆(定理1的逆定理)。
定义1 圆与无穷远直线的交点 ,称为平面上的圆点。
,称为平面上的圆点。
显然,两圆点的线坐标方程为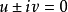 或
或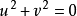 。
。
定义2 过平面内任意一点至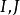 两点的两条直线,称为该点的迷向直线(极小直线)2。
两点的两条直线,称为该点的迷向直线(极小直线)2。
由定义可知,平面内任一点都有两条迷向直线,因而,平面内所有的点的迷向直线构成以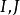 为中心的两个平行线束。因此,平面内只有两个迷向方向。当然它们都是虚直线,实际上是画不出来的。
为中心的两个平行线束。因此,平面内只有两个迷向方向。当然它们都是虚直线,实际上是画不出来的。
分类以k为斜率的直线上的无穷远点的坐标是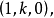 由此可知,两条迷向直线的斜率分别为
由此可知,两条迷向直线的斜率分别为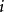 和
和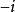 ,所以迷向直线的方程分别为
,所以迷向直线的方程分别为
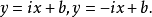
从而迷向方向分为两类,一类是斜率是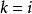 的,另一类是
的,另一类是 的2。
的2。
相关定理定理3每一条迷向直线与任意一条直线的交角是不确定的2。
证明:(1)设有两条同类迷向直线,它们的斜率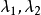 同为
同为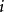 (或
(或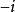 ),则
),则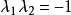 。由两条直线的交角公式
。由两条直线的交角公式
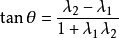 得知
得知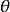 是不定的(
是不定的(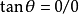 )。
)。
(2) 设有一条迷向直线,斜率为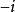 ,另一条是不同类的迷向直线或不是迷向直线,斜率为
,另一条是不同类的迷向直线或不是迷向直线,斜率为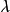 (
(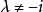 ),则由交角公式得
),则由交角公式得
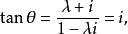 从而有
从而有
 即
即
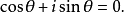 不论
不论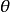 为实数或复数,应用欧拉公式,则
为实数或复数,应用欧拉公式,则
 设
设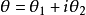 (
( 为实数),即有
为实数),即有
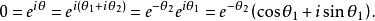 对于一切
对于一切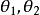 ,右端不可能为零,即
,右端不可能为零,即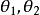 均不存在,故
均不存在,故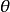 不存在。所以交角是不定的。
不存在。所以交角是不定的。
从定理3知,迷向直线的方向不能用角度表示,只能用斜率来表示。
定理4 (拉格尔Laguerre,1834-1886)设两条非迷向直线的交角为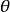 ,这两条直线与过其交点的两条以
,这两条直线与过其交点的两条以 为斜率的迷向直线所成的交比为
为斜率的迷向直线所成的交比为 ,则在对数函数的主值范围内必有
,则在对数函数的主值范围内必有
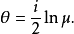
定理5两条非迷向直线垂直的充要条件是这两条直线被过交点的两条迷向直线调和共轭2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国