牛顿逼近法-牛顿逼近法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。1
简介牛顿逼近法,又称牛顿法(英语:Newton's method)又称为牛顿-拉弗森方法(英语:Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。方法使用函数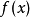 的泰勒级数的前面几项来寻找方程
的泰勒级数的前面几项来寻找方程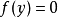 的根。
的根。
起源牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿去世后的1736年公开发表)中提出。约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。
方法说明蓝线表示方程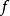 而红线表示切线。可以看出
而红线表示切线。可以看出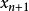 比
比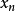 更靠近
更靠近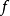 所要求的根
所要求的根 。
。
首先,选择一个接近函数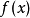 零点的
零点的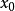 ,计算相应的
,计算相应的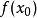 和切线斜率
和切线斜率 (这里
(这里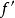 表示函数
表示函数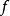 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点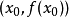 并且斜率为
并且斜率为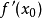 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:
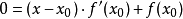
我们将新求得的点的 坐标命名为
坐标命名为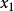 ,通常
,通常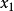 会比
会比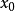 更接近方程
更接近方程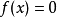 的解。因此可以利用
的解。因此可以利用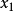 开始下一轮迭代。迭代公式可化简为如下所示:
开始下一轮迭代。迭代公式可化简为如下所示:
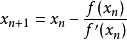
已经证明,如果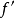 是连续的,并且待求的零点
是连续的,并且待求的零点 是孤立的,那么在零点
是孤立的,那么在零点 周围存在一个区域,只要初始值
周围存在一个区域,只要初始值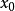 位于这个邻近区域内,那么牛顿法必定收敛。
位于这个邻近区域内,那么牛顿法必定收敛。
并且,如果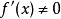 ,那么牛顿法将具有平方收敛的性能。粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍2。
,那么牛顿法将具有平方收敛的性能。粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍2。
具体介绍求代数方程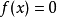 的精确解是很难的事情,特别地当
的精确解是很难的事情,特别地当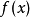 是 高于5次的多项式时,不能通过多项式系数的有限次运算得到根的表达式。在这种情况下求 方程的近似解却是可以的,牛顿法就是一种比较好的逐次逼近法。牛顿法在求根过程中逼近很快,用计算机计算是十分方便的。
是 高于5次的多项式时,不能通过多项式系数的有限次运算得到根的表达式。在这种情况下求 方程的近似解却是可以的,牛顿法就是一种比较好的逐次逼近法。牛顿法在求根过程中逼近很快,用计算机计算是十分方便的。
牛顿法的本质仍然是“以直代曲”,首先猜测一个值x1,用它近似方程的根 c,用过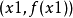 点的切线
点的切线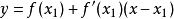 近似代替曲线
近似代替曲线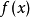 ,然后用切线方程
,然后用切线方程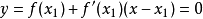 的根
的根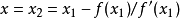 近似代替曲线方程的根c,这样就得到c的第二个近似值。依此类推可得到迭代公式
近似代替曲线方程的根c,这样就得到c的第二个近似值。依此类推可得到迭代公式
在复平面上选定一个区域,对于任意初始点(除去(0,0)点),讨论它在牛顿法迭代过程中的行为。一般选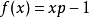 ,其中p是大于2的正整数。这样,迭代公式还可以 改写为
,其中p是大于2的正整数。这样,迭代公式还可以 改写为
对于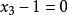 ,有三个根:
,有三个根: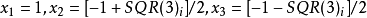 ,三个根均匀地分布在单位圆上3。
,三个根均匀地分布在单位圆上3。
迭代过程照例要先将复数分解为实部和虚部:
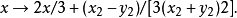
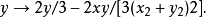
以 为例,用牛顿法生成分形图形的一个简单的matlab源程序如下:
为例,用牛顿法生成分形图形的一个简单的matlab源程序如下:
% 牛顿求根法
N=160;
warning off
[X,Y]=meshgrid((-N:N)/N*2);
[m,n]=find(X==0&Y==0);
X(m,n)=1;
Y(m,n)=1;
R=zeros(321);
G=R;
B=R;
for k=1:30;
Xn=2*X/3+(X.^2-Y.^2)./(3*(X.^2+Y.^2));
Yn=2*Y/3-2*X.*Y./(3*(X.^2+Y.^2));
X=Xn;
Y=Yn;
end
R(X>0.8)=1;
G(Y0.5)=1;
imshow(cat(3,R,G,B))
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国