[科普中国]-一次方程- · 科普中国网

一次方程也被称为线性方程，因为在笛卡尔坐标系上任何一个一次方程的表示都是一条直线，因此组成一次方程的每个项必须是常数或者是一个常数和一个变量的乘积，且方程中必须包含一个变量。因为如果没有变量只有常数的式子是算数式而非方程式。

定义一次方程式也被称为线性方程，因为在笛卡尔坐标系上任何一个一次方程的表示都是一条直线。组成一次方程的每个项必须是常数或者是一个常数和一个变量的乘积。且方程中必须包含一个变量，因为如果没有变量只有常数的式子是代数式而非方程式。

如果一个一次方程中只包含一个变量（x），那么该方程就是一元一次方程。如果包含两个变量（x和y），那么就是一个二元一次方程，以此类推。

一元一次方程一元一次方程式是指一个方程式中仅含有一个变量，且等号两边至少有一个一次单项式的方程。1

任意一个一元一次方程形式经化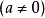的方程。它的解为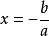以下就是一个例子：

x-17=-17x+3.

它的解便是：

20x=20.

x=1.

一元一次方程式是等于一条线性方程式：简单点来说，如 x2 或以上的次方是不容许的。

**注意：**当a=0时

ax+b=0不是一元一次方程式。

如果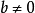，此方程式无限多解；如果 b=0，则此方程式恰一解。

二元一次方程求解二元一次联立方程式可以使用代入消去法或加减消去法。2

代入消去法代入消去法就是先利用其中一个方程，将含有其中一个未知数的代数式表示另一个未知数。然后代入另一个方程，从而将这组方程转化成解两个一元一次方程式的方法。

例如：

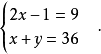
解2x-1=9.

得x=5.

再代入x+y=36.

即5+y=36.

从而求出y=36-5=31.

加减消去法加减消去法就是将两个方程加或相减，从而消去其中一个未知数的方法。

通常，我们先将其中一个方程的两边同时乘以一个不是0的数，使其中的一个系数与另外一个方程的对应系数相同。再将两个方程相加或相减。

例如：

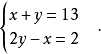
把两式相加消去x，即

y+2y=13+2.

从而求出

y=5.

线性化通常线性方程在实际应用中写作：

y=f(x).

这里f有如下特性：

f(x+y)=f(x)+f(y).

f(ax)=af(x).

这里a不是向量。

一个函数如果满足这样的特性就叫做线性函数，或者更一般的，叫线性化。

因为线性的独特属性，在同类方程中对线性函数的解决有叠加作用。这使得线性方程最容易解决和推演。

线性方程在应用数学中有重要规律。使用它们建立模型很容易，而且在某些情况下可以假设变量的变动非常小，这样许多非线性方程就转化为线性方程。

微分若y=Ax+B，则。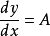

所以，线性函数并无驻点，即没有极大值和极小值，且线性函数的斜率是未知数 x的系数。