预序关系(简称预序,又称先序,preorder,quasi-order)、在数学中,是一类接近于偏序关系的二元关系,但仅满足自反性和传递性而不满足反对称性。偏序的大多数理论均可扩展到预序。
定义考虑集合 P 及其上的二元关系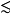 。若具有自反性和传递性,则称为预序。具体来说,对 P 的任意元素 a,b 和 c,下列性质成立:1
。若具有自反性和传递性,则称为预序。具体来说,对 P 的任意元素 a,b 和 c,下列性质成立:1
自反性:a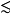 a
a
传递性:若a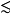 b且b
b且b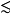 c,则a
c,则a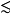 c
c
带预序的集合称为预序集合(preordered set,或者proset)。
同时满足反对称性(若 a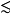 b 且 b
b 且 b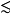 a,则 a = b)的预序为偏序。
a,则 a = b)的预序为偏序。
另一方面,如果一个预序满足对称性(若a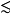 b,则b
b,则b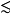 a),则为等价关系。
a),则为等价关系。
说明作为特例,空集上的空关系为一预序。空集加上空关系构成一预序集。
导出偏序将预序集的等价元素等同起来,可得到由该预序集所导出的偏序集。具体过程如下:定义预序集 X 上的等价关系 ,使得 a
,使得 a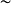 b 当且仅当 a
b 当且仅当 a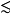 b 且 b
b 且 b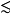 a。定义所得商集
a。定义所得商集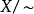 (所有
(所有 的等价类构成的集合)上的序关系
的等价类构成的集合)上的序关系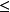 ,使得[x]
,使得[x]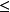 [y] 当且仅当 x
[y] 当且仅当 x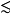 y。由
y。由 的构造可知,
的构造可知,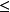 的定义与所选等价类的代表元素无关,故上述定义明确。易证该关系为一偏序。
的定义与所选等价类的代表元素无关,故上述定义明确。易证该关系为一偏序。
举例有向图(可以包括圈)上的可到达关系给出了一个预序≤,对于有向图中的任意两点x, y,x≤y当且仅当存在一条由x到y的路径。反过来说,每个预序都可理解为一个有向图上的可到达关系。(比如,如果x≤y的话,就规定这个图包含由x到y的有向边。)不过,这种对应关系不是唯一的。不同的图也可以给出相同的可到达关系。而同样地,有向无环图上的可到达关系也诱导出一个偏序。
拓扑中网的收敛定义使用预序比使用偏序可避免重要特征的丢失。
可数全序间的嵌入(embedding)关系。
图论中的graph-minor关系。
全预序的例子:一般模型中的偏好概念。
参见二元关系
偏序关系
全序关系
等价关系
有向集合
预序范畴
预良序
本词条内容贡献者为:
何星 - 副教授 - 上海交通大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国