[科普中国]-双锥台

在几何学中，双锥台又称双平截头体（英语：Bifrustum）是指三个相似的平形的平面图形如同锥体或柱体构造其侧面使图形封闭，通常中间的面最大，上下二个面等大，但较中间面小，或是指一个双锥体被两个平行平面，一个在赤道面上方、一个在赤道面下方所截后，位于两个平行平面之间的立体，或是可以看做是二个锥台以相同的底面相皆后所形成的几何图形，第三种者定义较广，包含凹双锥台，第二种者只包含凸双锥台，但也有上下不对称的双锥台。就如同锥台，双锥台也可以依据所截的是双圆锥还是双棱锥，可分为双圆台与双棱台。

双锥台可以视为双锥体截去二个极点，因此也可以称为截角双锥体或截顶双锥体。

双锥台的对偶多面体是双角锥柱。

双锥台也是一种分子构形。

双锥台的形状一般来说双锥台具有2n个梯形，2n个多边形，并且对偶为双角锥柱。1

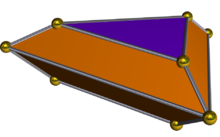
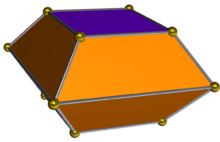
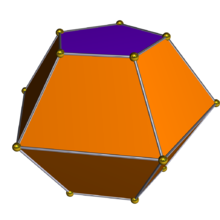
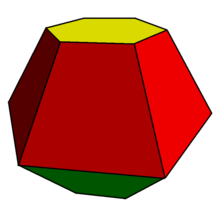
公式体积公式棱台或圆台的体积是原立体图形的体积减去被截去部分的体积：

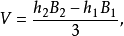B1指一个底面的面积，B2指另一个底面的面积,andh1，h2指原顶点分别到两底面的面积。考虑到：

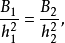这个体积也可用平截头体的高h=h2−h1与两底面面积的希罗平均数表达：

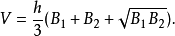
亚历山大里亚的希罗推导出了这个公式并且凭借它遇到了虚数。

特别地，圆台的体积是：

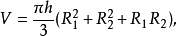π等于3.14159265...，R1,R2是两底面的半径。

底面为n边形的棱台的体积是：

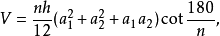a1与a2是底面的边长。

表面积公式对于一个正圆台，

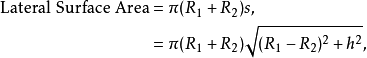
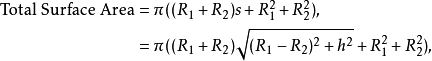LateralSurfaceArea指侧面积，TotalSurfaceArea指总面积，R1andR2为底面半径，s为平截头体的斜高。一个底面为正n边形的正棱台的表面积是：

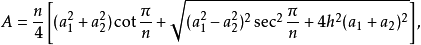a1与a2是两底面的边长。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学