在数学中,正合序列、正合列或译作恰当序列于同调代数中居于核心地位,其中特别重要的一类是短正合序列。
定义一个由某类适宜的范畴(例如阿贝尔群、向量空间或模,详如后述)中的对象与态射构成的序列
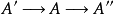 被称作在
被称作在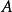 处正合,当且仅当
处正合,当且仅当
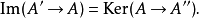 一般而言,该范畴中的序列
一般而言,该范畴中的序列
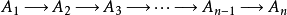 被称作是正合的,当且仅当它在
被称作是正合的,当且仅当它在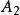 、
、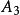 、
、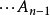 处正合。类似定义可以推广至没有端点的无穷序列。
处正合。类似定义可以推广至没有端点的无穷序列。
为了探讨序列的正合性,范畴中必须能构造一个态射的像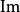 与核
与核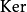 ,并确保这两种构造具备在阿贝尔群、向量空间或模的情形一样的范畴论性质。处理这类问题的框架是阿贝尔范畴,以下考虑的范畴如未说明皆为阿贝尔范畴。1
,并确保这两种构造具备在阿贝尔群、向量空间或模的情形一样的范畴论性质。处理这类问题的框架是阿贝尔范畴,以下考虑的范畴如未说明皆为阿贝尔范畴。1
例子1、序列
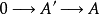 正合的充要条件是
正合的充要条件是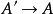 是单射。
是单射。
2、序列
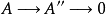 正合的充要条件是
正合的充要条件是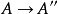 是满射。
是满射。
3、对任何态射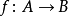 ,以下序列都是正合的:
,以下序列都是正合的:
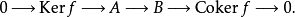 注意:在群的范畴中,必须要求
注意:在群的范畴中,必须要求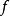 在
在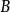 中的像是正规子群才能考虑
中的像是正规子群才能考虑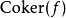 ,故上述正合性对一般范畴不成立。1
,故上述正合性对一般范畴不成立。1
短正合序列一个具下述形式的正合序列:
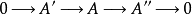 称作短正合序列。
称作短正合序列。
分裂短正合序列若以下任一等价条件成立,则称短正合序列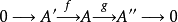 分裂:
分裂:
1、有截面(即存在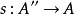 使得
使得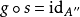 )。
)。
2、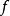 有缩回(即存在
有缩回(即存在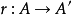 使得
使得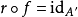 )。
)。
3、该短正合序列同构(在链复形的意义下)于
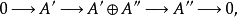 其中的箭头是直和的典范映射。
其中的箭头是直和的典范映射。
对于群的范畴,前两个条件不一定蕴含第三个,它们只能保证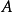 可以表为
可以表为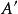 与
与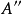 的半直积;例如我们可考虑群同态
的半直积;例如我们可考虑群同态
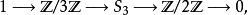 其中
其中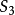 是3次对称群。
是3次对称群。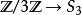 由
由 给出,它的像是交代群
给出,它的像是交代群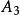 ,商为
,商为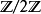 ;但
;但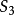 无法分解成
无法分解成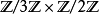 。
。
将正合序列拆解为短正合序列正合序列可以透过核Ker与上核Coker的构造拆解为短正合序列,构造方式如下:考虑一正合序列
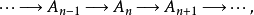 设
设
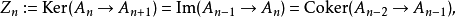 其中
其中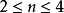 ,这就给出了一个短正合序列
,这就给出了一个短正合序列
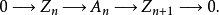
一般而言,设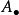 为链复形,我们同样定义
为链复形,我们同样定义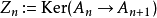 ;此时链复形的正合性等价于所有短链
;此时链复形的正合性等价于所有短链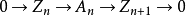 的正合性。
的正合性。
推广给定一个短正合序列
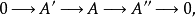 有时也称
有时也称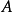 为
为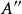 经由
经由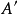 的扩张。2
的扩张。2
长正合序列若有链复形的短正合序列:
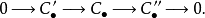 反复运用蛇引理,可以导出正合序列:
反复运用蛇引理,可以导出正合序列:
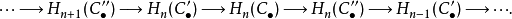 对上链复形的上同调亦同,此时连接同态的方向是
对上链复形的上同调亦同,此时连接同态的方向是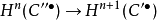 。这类序列称作长正合序列,它是同调代数最重要的技术之一。在代数拓扑中,长正合序列与相对同调群和Mayer-Vietoris序列相关。导函子也可以导出相应的长正合序列。2
。这类序列称作长正合序列,它是同调代数最重要的技术之一。在代数拓扑中,长正合序列与相对同调群和Mayer-Vietoris序列相关。导函子也可以导出相应的长正合序列。2
参见正合函子
链复形
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国