鉴于最小平方误差(Mean Square error)和峰值信噪比(Peak signal-to-noise ratio)无法完全反应人类视觉上所感受的误差,学者在2004年提出了结构相异性(structural dissimilarity)这一新的误差测量方法。
定义假设有两个信号x与y,它们的结构相异性为
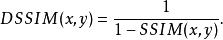
其中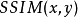 为x与y的结构相似性。1
为x与y的结构相似性。1
结构相似性两者的结构相似性定义为:
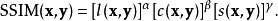
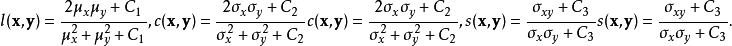 其中,
其中,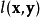 比较
比较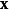 和
和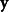 的亮度(luminance),
的亮度(luminance),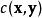 比较
比较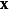 和
和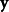 的对比度,
的对比度,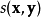 比较
比较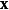 和
和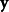 的结构(structure),
的结构(structure),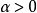 ,
,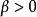 ,
,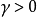 ,为调整
,为调整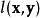 、
、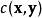 、
、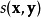 相对重要性的参数,
相对重要性的参数,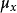 及
及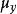 、
、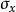 及
及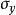 分别为
分别为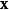 和
和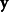 的平均值和标准差,
的平均值和标准差,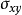 为
为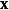 和
和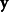 的共变异数,
的共变异数,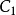 、
、 、
、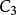 皆为常数,用以维持
皆为常数,用以维持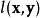 、
、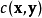 、
、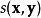 的稳定。
的稳定。
结构相似性指标的值越大,代表两个信号的相似性越高。
若使用相同的两张图片去做SSIM运算,也就是说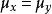 且
且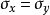 ,可以得到
,可以得到
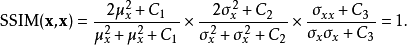
实际使用时,简化起见,一般会将参数设为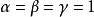 及
及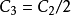 ,得到:
,得到:
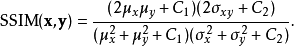
在计算两张影像的结构相似性指标时,会开一个局部性的视窗,一般为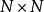 的小区块,计算出视窗内信号的结构相似性指标,每次以像素为单位移动视窗,直到整张影像每个位置的局部结构相似性指标都计算完毕。将全部的局部结构相似性指标平均起来即为两张影像的结构相似性指标。2
的小区块,计算出视窗内信号的结构相似性指标,每次以像素为单位移动视窗,直到整张影像每个位置的局部结构相似性指标都计算完毕。将全部的局部结构相似性指标平均起来即为两张影像的结构相似性指标。2
结构相异性的范围当DSSIM越大时,代表两张图片越接近,SSIM越接近1,DSSIM的值也越大,当SSIM=1,也就是DSSIM趋近无限时,和原始视讯档案完全一致,若SSIM>=0.98就是难以与原始视讯档案分辨区别,而SSIM=0.95的时候大多数人都会对画面满意,这个数值可以认为是及格的画面。SSIM=0.90的时候意味着瑕疵可能要比0.95多一倍,肉眼就会察觉到明显的画面劣化,因此低于这个数值时,就可以判定为没有实际观赏价值。2
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国