数学中的逼近理论是如何将一函数用较简单的函数来找到最佳逼近,且所产生的误差可以有量化的表征,以上提及的“最佳”及“较简单”的实际意义都会随着应用而不同。
简介数学中有一个相关性很高的主题,是用广义傅立叶级数进行函数逼近,也就是用以正交多项式为基础的级数来进行逼近。
计算机科学中有一个问题和逼近理论有关,就是在数学函式库中如何用计算机或计算器可以执行的功能(例如乘法和加法)尽可能的逼近某一数学函数,一般会用多项式或有理函数(二多项式的商)来进行。
逼近理论的目标是尽可能的逼近实际的函数,一般精度会接近电脑浮点运算的精度,一般会用高次的多项式,以及(或者)缩小多项式逼近函数的区间。缩小区间可以针对要逼近的函数,利用许多不同的系数及增益来达到。数学函式库将区间划分为许多的小区间,每个区间搭配一个次数不高的多项式。1
最佳多项式只要选定了多项式的次数及逼近的范围,就可以用以使最坏情形误差最小化的原则,来选择逼近多项式,其目的为最小化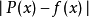 的绝对值,其中P(x)为逼近多项式,而f(x)为实际的函数。对于一个良态的函数,存在一个N次的多项式,使误差曲线的大小在
的绝对值,其中P(x)为逼近多项式,而f(x)为实际的函数。对于一个良态的函数,存在一个N次的多项式,使误差曲线的大小在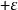 和
和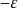 之间震荡至多N+2次,其最坏情形的误差为
之间震荡至多N+2次,其最坏情形的误差为 。一个N次的多项式可以内插曲线中的N+1个点。当然也有可能制造一些极端的函数,使得满足上述条件的多项式不存在,但在实务上很少需要为这様的函数进行逼近。
。一个N次的多项式可以内插曲线中的N+1个点。当然也有可能制造一些极端的函数,使得满足上述条件的多项式不存在,但在实务上很少需要为这様的函数进行逼近。
例如右图中的红线就是用N=4情形下用多项式逼近log(x)及exp(x)的误差。误差在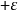 和
和 之间震荡。每一个例子中的极端有N+2个,也就是6个。极值出现在区间的端点,也就是图的最左边及最右边。1
之间震荡。每一个例子中的极端有N+2个,也就是6个。极值出现在区间的端点,也就是图的最左边及最右边。1
切比雪夫近似切比雪夫近似是利用将函数展开为由切比雪夫多项式组成的各项,依需要的逼近程度决定展开的项次,可以得到很接近多项式的结果。此作法类似进行函数的傅立叶分析,只是用切比雪夫多项式代替分析中用到的三角函数。
若计算一函数切比雪夫展开的系数:
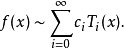 只展开到
只展开到 项为止,可以得到一个逼近f(x)的N次多项式。
项为止,可以得到一个逼近f(x)的N次多项式。
对于一个有快速收敛幂级数的函数而言,若展开到一定项次后截止不再展开,截止产生的误差接近截止后的第一项,因此误差可以由截止后的第一项代表。若是用切比雪夫多项式展开,也会有一様的结果。若切比雪夫展开只展开到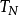 ,后面截止,其误差会接近
,后面截止,其误差会接近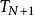 的整数倍。切比雪夫多项式的特点是在[−1, 1]区间以内.其数值会在+1和−1之间震荡。
的整数倍。切比雪夫多项式的特点是在[−1, 1]区间以内.其数值会在+1和−1之间震荡。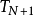 有N+2个极点。因此f(x)和切比雪夫展开的误差接近一个有N+2个极点的函数,因此为近似最佳的N次多项式。
有N+2个极点。因此f(x)和切比雪夫展开的误差接近一个有N+2个极点的函数,因此为近似最佳的N次多项式。
在上面中,可以看到蓝色线(切比雪夫近似的误差)有时比红色线(最佳多项式的误差)接近x轴,但有时蓝色线反而离x轴较远,因此切比雪夫近似和最佳多项式毕竟还是有差异。不过exp函数是快速收敛的函数,切比雪夫近似的误差会比log函数要好。
切比雪夫近似是数值积分方法Clenshaw–Curtis正交法的基础。12
雷米兹算法雷米兹算法是在1934年由苏俄数学家雷米兹提出的算法。可用来产生在一定区间内逼近函数f(x)的最佳多项式P(x)。雷米兹算法是一种迭代式的算法,最后会收敛到使误差函数N+2个极值的多项式。
雷米兹算法是用以下的事实为基础:可以在有N+2个测试点的情形下,创建一个N次多项式,其误差函数在0附近震荡。
假设N+2个测试点 (其中
(其中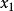 和
和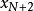 假设是区间的二个端点),需求解以下的多项式:
假设是区间的二个端点),需求解以下的多项式:
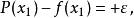
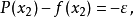
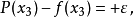
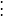
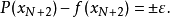 等式右侧的正负号交替出现。因此可以得到下式:
等式右侧的正负号交替出现。因此可以得到下式:

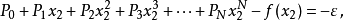

既然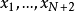 给定,其各次方的幂次也是已知,而
给定,其各次方的幂次也是已知,而 也是已知。上式就变成由N+2的线性方程组成的联立方程.有N+2个变数,分别是
也是已知。上式就变成由N+2的线性方程组成的联立方程.有N+2个变数,分别是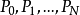 及
及 。可以解出上式的多项式P及误差
。可以解出上式的多项式P及误差 。1
。1
相关条目切比雪夫多项式
广义傅立叶级数
正交多项式
正交基
傅里叶级数
邵德尔基
帕德逼近
函数逼近
样条函数1
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国