[科普中国]-完全相关

完全相关是指两个变量之间的关系，一个变量的数量变化由另一个变量的数量变化唯一确定。其相关系数为+1或-1。

基本内容现象之间的数量关系存在着两种不同的类型：一种是函数关系，另一种是相关关系。

函数关系指的是变量之间存在着的严格的依存关系，它们之间的关系值是固定的，对于某一变量的每一个值，都有另一个变量的完全确定的值与之相对应。例如，圆的面积等于圆周率乘以半径的平方。

相关关系是指变量之间确实存在的但关系值不固定的相互依存关系。在这种关系中，当一个(或几个)变量的值确定以后，另一个变量的值虽与它(或它们)有关，但却不能完全确定。这是一种非确定性的关系。例如，电视机的拥有率与人均收入水平有关，但对于人均收入水平相同的地区，其电视机的拥有率可能不尽相同。

在相关关系中，通常，在相互联系的现象之间存在着一定的因果关系，这时就把其中的起着影响作用的现象具体化，通过一定的变量反映出来，这样的变量称为自变量。由于受到自变量变动的影响而发生变动的变量称为因变量。例如，在粮食亩产量与施肥量之间，施肥量这一变量是自变量，亩产量这一变量是因变量。1

比较相关关系按方向分为正相关和负相关。正相关是指两个变量的变化趋势相同，从散点图可以看出各点散布的位置是从左下角到右上角的区域，即一个变量的值由小变大时，另一个变量的值也由小变大。负相关是指两个变量的变化趋势相反，从散点图可以看出各点散布的位置是从左上角到右下角的区域，即一个变量的值由小变大时，另一个变量的值由大变小。

相关关系按形式分为线性相关和非线性相关。线性相关（直线相关）是指当相关关系的一个变量变动时，另一个变量也相应地发生均等的变动。非线性相关（曲线相关）是指当相关关系的一个变量变动时，另一个变量也相应地发生不均等的变动。

相关关系按变量数目分为单相关、复相关和偏相关。单相关是指只反映一个自变量和一个因变量的相关关系。复相关是指反映两个及两个以上的自变量同一个因变量的相关关系。偏相关是指当研究因变量与两个或多个自变量相关时，如果把其余的自变量看成不变（即当作常量），只研究因变量与其中一个自变量之间的相关关系，就称为偏相关。

相关关系按程度分为完全相关、不完全相关和完全不相关。完全相关是指两个变量之间的关系，一个变量的数量变化由另一个变量的数量变化唯一确定。不完全相关是指两个变量之间的关系介于不相关和完全相关之间。完全不相关是指如果两个变量彼此的数量变化互相独立，没有关系。2

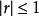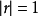表示两个变量之间线性相关程度的描述通常采用相关系数，用r表示。用来说明在线性相关条件下两个变量之间相关关系密切程度的指标。相关系数 。特别当 时，称它们是完全相关的。当 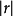较小而接近于0时，它们的相关关系很弱，特别当 r=0时，称它们线性无关。相关系数r只表明x与y之间的线性关系的密切程度和方向。当r很小甚至为0时，只表明x与y之间的线性关系不密切，或不存在线性关系，并不表示x与y之间就没有关系，可能二者之间有非线性关系。3

相关例题例1.当相关系数r=（）时，x和y之间符合直线函数关系，称x与y完全相关。

A．+1；

B．-1；

C．±1；

D．接近1。

解：两个变量之间线性相关程度的描述通常采用相关系数，用r表示。特别当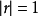 时，称它们是完全相关的。故选C。

例2.当x和y的r取-1时，两者为哪种相关关系？x和y的r取1时，两者为哪种相关关系？

解：当x和y的r取-1时，两者为完全负相关关系。x和y的r取1时，两者为完全正相关关系。

教学应用在完全相关的数学教学中可以采用“探究法”。“探究法”的精髓在于以学生为主角，使他们由被动地接受知识转变为知识的探索者。通过亲自动手，积极思考，热烈讨论，探索知识，学生能更加深入理解知识的内涵，并培养观察力、思维能力、动手能力、归纳能力、语言表达能力和创造能力等。“探究式教学法 ”是指在老师的指导下 ，学生通过具体的操作，亲自尝试后，经过积极思考和讨论，找到知识的规律，总结出结论，学会新知，并发展思维、培养能力的综合教学方法。通过让学生对不同种类的相关关系进行区分，可以引导学生对完全相关进行积极思考，从而使学生从本质上了解完全相关，最终明确完全相关是指两个变量之间的关系，一个变量的数量变化由另一个变量的数量变化唯一确定这一基本概念，从中拓展学生思维、提高学生独立思考的能力。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学