[科普中国]-位似三角形

位似三角形是指两个每组对应顶点所在的直线都交于一点，对应边互相平行的相似三角形。

基本内容位似图形：如果两个相似图形的每组对应顶点所在的直线都交于一点，对应边互相平行，那么这样的两个图形叫做位似图形。

位似中心：两个位似图形中每组对应顶点所在的直线都交于一点，这个交点叫做位似中心。

位似比：新图形与原图形的对应边的长度之比。即位似图形的相似比。

两个三角形对应顶点的连线相交于一点且到各对应点成比例的两个相似三角形，且两个三角形的各边分别平行，这样的两个三角形即为位似三角形。1

条件1.两个三角形相似；

2.两个三角形每组对应点的连线在一点；

3.两个三角形对应边互相平行。

三条件缺一不可，否则不是位似三角形。2

性质相似三角形具有如下性质：

①对应角相等；

②对应边、对应高、对应中线、对应角的平分线以及周长等，它们的比都等于相似比；

③面积的比等于相似比的平方。

位似三角形不仅具有相似三角形的所有性质，而且还有如下性质：

①任意一对对应点到位似中心的距离之比都等于相似比，这个相似比也可称为位似比；

②对应线段互相平行。2

画图步骤1.确定位似中心；

2.分别连接并延长位似中心和能代表原图的关键点；

3.根据相似比，确定能代表所作的位似三角形的关键点；

4.顺次连接上述各点，得到放大或缩小的图形。3

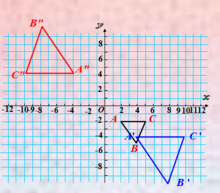
相关计算例1.△ABC三个顶点坐标分别为A（2，－2），B（4，－5），C（5，－2），以原点O为位似中心，将这个三角形放大为原来的2倍。

解：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k。所以对应点的坐标为A′（4 ，-4），B ′ （8，-10），C ′（10，-4）或A" （-4，4）B" （-8，10），C" （-10，4）。如图1所示。

应用教学在位似三角形的数学教学中可以采用“探究法”。“探究法”的精髓在于以学生为主角，使他们由被动地接受知识转变为知识的探索者。通过亲自动手，积极思考，热烈讨论，探索知识，学生能更加深入理解知识的内涵，并培养观察力、思维能力、动手能力、归纳能力、语言表达能力和创造能力等。“探究式教学法 ”是指在老师的指导下 ，学生通过具体的操作，亲自尝试后，经过积极思考和讨论，找到知识的规律，总结出结论，学会新知，并发展思维、培养能力的综合教学方法。通过让学生对位似图形进行进一步了解，可以引导学生对位似图形中的位似三角形进行积极思考，从而使学生从本质上了解位似三角形的基本内容，最终明确两个相似三角形的每组对应顶点所在的直线都交于一点，对应边互相平行的两个三角形为位似三角形这一概念，从中拓展学生思维、提高学生独立思考的能力。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学