集合运算,是数学科学中常用的词语,是一种非常有效的构造形体的方法,可以直观的减少运算难度。
概念集合运算是实体造型系统中非常重要的模块,也是一种非常有效的构造形体的方法。从一维几何元素到三维几何元素,人们针对不同的情况和应用要求,提出了不少集合运算算法。
在早期的造型系统中,处理的对象是正则形体,因此定义了正则形体集合运算,来保证正则形体在集合运算下是封闭的。在非正则形体造型中,参与集合运算的形体可以是体、面、边、点,运算的结果也是这些形体,这就要求集合运算算法中能统一处理这些不同维数的形体,因此需要引入非正则形体运算。
1、正则集与正则集合运算算子
Tilove根据点集拓扑学的原理,给出了正则集的定义。认为正则的几何形体是由其内部点的闭包构成,即由内部点和边界两部分组成。对于几何造型中的形体,规定正则形体是三维欧氏空间中的正则集合,因此可以将正则几何形体描述如下:
主要类型设G是三维欧氏空间R3中的一个有界区域,且G=bG∪iG,其中bG是G的n-1维边界,iG是G的内部。G的补空间cG称为G的外部,此时正则形体G需满足:
1)bG将iG和cG分为两个互不连通的子空间;
2)bG中的任意一点可以使iG和bG连通;
3)bG中任一点存在切平面,其法矢指向cG子空间
4)bG是二维流形。
对于正则形体集合,可以定义正则集合算子。设是集合运算算子(交、并或差),如果R3中任意两个正则形体A、B作集合运算:
R=AB
运算结果R仍是R3中的正则形体,则称为正则集合算子,正则并、正则交、正则差分别记为∪*,∩*、-*1。
分类几何造型中的集合运算实质上是对集合中的成员进行分类的问题,Tilove给出了集合成员分类问题的定义及判定方法。
Tilove对分类问题的定义为:设S为待分类元素组成的集合,G为一正则集合,则S相对于G的成员分类函数为:
C(S,G)={S in G,S out G,S on G}, (3-2-1)
其中,
S in G=S∩iG,
S out G=S∩cG,
S on G=S∩bG,
如果S是形体的表面,G是一正则形体,则定义S相对于G的分类函数时,需考虑S的法向量。记-S为S的反向面。形体表面S上一点P相对于外侧的法向量为NP(S),相反方向的法向量为- NP(S),则(3-2-1)式中S on G可分为两种情况:
S on G ={S shared(bG),S shared(-bG)},
其中,
S shared(bG)={P|P∈S,P∈bG,NP(S)=NP(bG)},
S shared(-bG)={P|P∈S,P∈bG,NP(S)=-NP(bG)}。
于是,S相对于G的分类函数C(S,G)可写为:
C(S,G)={S in G,S out G,S shared(bG),S shared(-bG)}。
由此,正则集合运算定义的形体边界可表达为:
b(A∪B)={bA out B,bB out A,bA shared(bB)},
b(A∩B)={bA in B,bB in A,bA shared(bB)},
b(A-B)={bA out B,-(bB in A),bA shared(-bB)}。
3.集合运算算法
正则集合运算与非正则形体运算的区别在于增加了正则化处理步骤。下面,我们给出一个非正则形体的集合运算算法。
假定参与集合运算的形体为A和B,运算的结果形体C=AB,其中集合运算符为通常的集合运算并、交、差(È 、Ç 、- )。
对于一个非正则形体L,可以将其分解为L=L3ÈL2ÈL1ÈL0,其中L3为R3中的正则闭集之并,存在面表、边表、点表等拓扑元素。L2是悬面集,存在边表和点表。L1是悬边集,只有端点。L0是孤立点集。
集合运算整个算法包括了以下几部分:
(1)求交:参与运算的一个形体的各拓扑元素求交,求交的顺序采用低维元素向高维元素进行。用求交结果产生的新元素(维数低于参与求交的元素)对求交元素进行划分,形成一些子元素。这种经过求交步骤之后,每一形体产生的子拓扑元素的整体相对于另一形体有外部、内部、边界上的分类关系。
2)成环:由求交得到的交线将原形体的面进行分割,形成一些新的面环。再加上原形体的悬边、悬点经求交后得到的各子拓扑元素,形成一拓扑元素生成集。
(3)分类:对形成的拓扑元素生成集中的每一拓扑元素,取其上的一个代表点,根据点/体分类的原则,决定该点相对于另一形体的位置关系,同时考虑该点代表的拓扑元素的类型(即其维数),来决定该拓扑元素相对于另一形体的分类关系。
(4)取舍:根据拓扑元素的类型及其相对另一形体的分类关系,按照集合运算的运算符要求,要决定拓扑元素是保留还是舍去;保留的拓扑元素形成一个保留集。
(5)合并:对保留集中同类型可合并的拓扑元素进行合并,包括面环的合并和边的合并。
(6)拼接:以拓扑元素的共享边界作为其连接标志,按照从高维到低维的顺序,收集分类后保留的拓扑元素,形成结果形体的边界表示数据结构2。
集合的运算并主条目:并集
两个集合可以相"加"。A和B的并集是将A和B的元素放到一起构成的新集合。
定义
给定集合A,B,定义运算∪如下:A∪B = {e|e∈A 或 e∈B}。A∪B称为A和B的并集。
A 和 B 的并集
示例
{1, 2}∪{红色, 白色} = {1, 2, 红色, 白色}
{1, 2, 绿色}∪{红色, 白色, 绿色} = {1, 2, 红色, 白色, 绿色}
{1, 2}∪{1, 2} = {1, 2}
基本性质
作为集合间的二元运算,∪运算具有以下性质。
交换律:A∪B = B∪A;
结合律:(A∪B)∪C = A∪(B∪C);
幂等律:A∪A = A;
幺元:∀集合A,A∪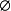 = A;(
= A;(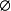 是∪运算的幺元)。
是∪运算的幺元)。
交主条目:交集
一个新的集合也可以通过两个集合"共"有的元素来构造。A和B的交集,写作A∩B,是既属于A的、又属于B的所有元素组成的集合。
若A∩B={\displaystyle \varnothing },则A和B称作不相交。
A 和 B 的交集
定义
给定集合A,B,定义运算∩如下:A∩B = {e|e∈A 且 e∈B}。A∩B称为A和B的交集。
基本性质
作为集合间的二元运算,∩运算具有以下性质。
交换律:A∩B = B∩A;
结合律:(A∩B)∩C = A∩(B∩C);
幂等律:A∩A = A;
空集合:∀集合A,A∩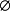 =
= 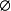 ;(
;(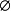 是∩运算的空集合)。
是∩运算的空集合)。
其它性质还有:
A⊆B ⇒ A∩B = A
示例
{1, 2}∩{红色, 白色} =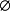
{1, 2, 绿色}∩{红色, 白色, 绿色} = {绿色}
{1, 2}∩{1, 2} = {1, 2}
差主条目:差集
两个集合也可以相"减"。A在B中的相对补集,写作B−A,是属于B的、但不属于A的所有元素组成的集合。
在特定情况下,所讨论的所有集合是一个给定的全集U的子集。这样,U−A称作A的绝对补集,或简称补集(余集),写作A′或CUA。
补集可以看作两个集合相减,有时也称作差集。
定义
给定集合A,B,定义运算-如下:A - B = {e|e∈A 且 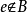 。A - B称为B对于A的差集,相对补集或相对余集。
。A - B称为B对于A的差集,相对补集或相对余集。
在上下文确定了全集U时,对于U的某个子集A,一般称U - A为A(对于U)的补集或余集,通常记为A'或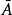 ,也有记为CUA的。
,也有记为CUA的。
基本性质
作为集合间的二元运算,- 运算有如下基本性质:
A - A = 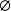 ;
;
右幺元:∀集合A,A -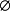 = A;(
= A;(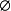 是 - 运算的右幺元)。
是 - 运算的右幺元)。
左零元:∀集合A,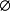 - A =
- A =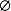 ;(
;(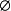 是 - 运算的左零元)。
是 - 运算的左零元)。
示例
{1, 2}−{红色, 白色} = {1, 2}
{1, 2, 绿色}−{红色, 白色, 绿色} = {1, 2}
{1, 2}−{1, 2} =
若U是整数集,则奇数的补集是偶数
对称差主条目:对称差
定义
给定集合A,B,定义对称差运算△如下:A△B = (A-B)∪(B-A)。
基本性质
作为集合间的二元运算,△运算具有如下基本性质:
交换律:A△B = B△A;
结合律:(A△B)△C = A△(B△C);
幺元:∀集合A,A△ 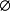 = A;(
= A;(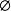 是△运算的幺元)。
是△运算的幺元)。
逆元:A△A =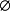 ;
;
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国