[科普中国]-伪相关

伪相关，这是统计学上的一个概念。实际上，在自然界里存在两种相关现象，除了真正的相关外,还有一种相关叫伪相关。太阳落山和月亮升起并没有什么因果关系，它只是地球自转的反映,但这两种现象确实是相关的,太阳落山的时候月亮正好升起，这就叫伪相关。

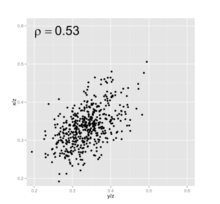
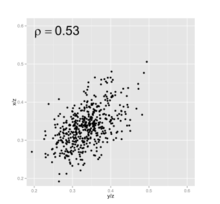
简介伪相关(Spurious correlation)的定义最早由Karl Spearman提出，用以描述两组由绝对测量值转换而来的比例数据之间的相关，如百分比、千分比等。Spearman举了一个简单的例子：x, y, z为三组彼此间不相关的数据，但将前两组数据与z相比后，将得出x/z与y/z中存在显著相关（如图1）。在另一张图（图2）中，我们以蓝色和红色分布标示较大或较小的分母z，会发现z较大的情况下，x/z与y/z较小，分布于左下，而较小的z对应着数值更大的x/z与y/z，可以说作为分母的z本身的影响，造成了x/z与y/z之间的线性分布，即使这三组数据间不存在任何关系。

在此我们了解到伪相关是指一种狭义的相关现象，而汉语民间语境中的伪相关，更多指的是另一统计术语“伪关系1”。

伪相关定义伪相关(spurious relationship)，又称伪关系、虚假关系，顾名思义是虚假的“关系”，但此处的关系指的是因果，而非相关，即两因素间本不存在因果关系，却被误认为存在。这种错误出现的原因包括忽略了第三方潜在因素的影响，如前文介绍伪相关的例子，地球自转对太阳落山与月亮上山的影响。严格意义上说，因为伪关系描述的是因果，如两事物间的本身不被认为有因果关系，那也不会是伪关系。根据一些学者的说法，伪关系是相关向因果迈进的必经阶段，排除了伪关系因素的相关研究才可能进一步探索因果关系。

对于伪关系的剔除目前主要有两种方法：实验与纯统计检验。前者通过尽可能控制其它潜在影响因素，操纵其中某一变量并观测另一变量的变化来明确两者间的关系；后者则更多应用于一些无法付诸实验而采用观测数据的学科，如经济学。

相关系数与伪相关两个变量可能会受第三者影响，从而在其间得出误导性的相关系数。当变量 A 和 B 有相关时，有几种可能：

A导致B；

B导致A；

C导致A和B。

第三种情况就会发生伪相关。如果在统计上控制住C变数，A和B就不再相关。

回归现象与伪相关当回归分析中B随A变化时，实际因果关系可能如下：

C → A → B；

A → C → B；

C → A；C → B。

示例例一

统计研究发现，冰淇淋销量最高的时候，就是公共泳池的溺水事故发生得最多的时候。

然而，有可能热浪造成冰淇淋销量和公共泳池的溺水事故增多。若视冰淇淋的销量或遇溺事故为对方的成因，可能就被伪关系误导了。

例二

荷兰的统计数字显示，在一连串的春季中，鹳鸟巢的数目与人类婴儿出生数目之间呈现正相关。

两者之间未必有因果关系。事实上，它们都和数据观测之前9个月的天气相关2。

实验伪相关一词常用于统计学上，特别是在实验的测定结果上。实验一般用以检测如“X → Y”的因果关系。然而两者的共同因素(W → X & Y)可造成非因果关系的相关。另外，如“X → W → Y”形的中介变数若没有察觉出来的话，两者非直接的关系便会看似是直接的。因此，除非能排除伪关系的可能性，否则实验得出的相关并不代表因果关系。

实际上，下列三个条件都要成立，才可以得出X导致Y的结论：

X发生在Y之前；

若X不发生则Y也不发生；

若X发生则Y一定发生。

如果上面三项中任何一项不符合，就可以确认出伪关系。

至于间接的因果关系，则不需要上列的第三项条件。例如，手枪决斗中，两个男人面对面，向对方开火。若其中一人击中对方，而对方死亡，则可以推断出他导致对方死亡。但是，若医生把受伤的男人救回（不符合第三项条件），这没有把因果关系终止，而只终止了直接的因果关系。由于开火X而导致身体受伤W，从而导致死亡Y。因为医生的救治，终止了从W至Y的关系。3

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学